scipy.stats.

yeojohnson#

scipy.stats.yeojohnson(x, lmbda=None)[源代码]#

返回通过 Yeo-Johnson 幂变换转换的数据集。

参数:
xndarray

输入数组。应为一维。

lmbdafloat, 可选

如果 lmbda 为 None，则找到最大化对数似然函数的 lambda，并将其作为第二个输出参数返回。否则，将对给定值进行转换。

返回值:
yeojohnson: ndarray

Yeo-Johnson 幂变换数组。

maxlogfloat, 可选

如果 lmbda 参数为 None，则第二个返回的参数是最大化对数似然函数的 lambda。

另请参阅

probplot, yeojohnson_normplot, yeojohnson_normmax, yeojohnson_llf, boxcox

注释

Yeo-Johnson 变换由下式给出

\[\begin{split}y = \begin{cases} \frac{(x + 1)^\lambda - 1}{\lambda}, &\text{for } x \geq 0, \lambda \neq 0 \\ \log(x + 1), &\text{for } x \geq 0, \lambda = 0 \\ -\frac{(-x + 1)^{2 - \lambda} - 1}{2 - \lambda}, &\text{for } x < 0, \lambda \neq 2 \\ -\log(-x + 1), &\text{for } x < 0, \lambda = 2 \end{cases}\end{split}\]

与 boxcox 不同, yeojohnson 不要求输入数据为正数。

1.2.0 版本新增。

参考文献

I. Yeo 和 R.A. Johnson, “一种改进正态性或对称性的新的幂变换族”, Biometrika 87.4 (2000)

示例

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

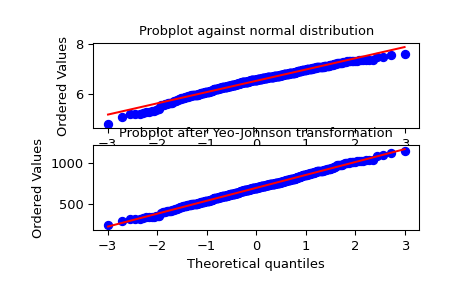
我们从一个非正态分布中生成一些随机变量，并为其制作一个概率图，以显示它在尾部是非正态的

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

我们现在使用 yeojohnson 转换数据，使其最接近正态

>>> ax2 = fig.add_subplot(212)
>>> xt, lmbda = stats.yeojohnson(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Yeo-Johnson transformation')

>>> plt.show()
../../_images/scipy-stats-yeojohnson-1.png
在本页