scipy.stats.

yeojohnson_llf

scipy.stats.yeojohnson_llf(lmb, data)

Yeo-Johnson 对数似然函数。

参数:

lmb标量

Yeo-Johnson 变换的参数。 有关详细信息，请参见yeojohnson。

dataarray_like

用于计算 Yeo-Johnson 对数似然的数据。 如果 data 是多维的，则沿第一个轴计算对数似然。

返回:

llffloat

给定 lmb 的 data 的 Yeo-Johnson 对数似然。

另请参阅

yeojohnson, probplot, yeojohnson_normplot, yeojohnson_normmax

注释

Yeo-Johnson 对数似然函数在此定义为

\[llf = -N/2 \log(\hat{\sigma}^2) + (\lambda - 1) \sum_i \text{ sign }(x_i)\log(|x_i| + 1)\]

其中 \(\hat{\sigma}^2\) 是 Yeo-Johnson 变换的输入数据 x 的估计方差。

在 1.2.0 版本中添加。

示例

在你的浏览器中尝试一下！

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1.inset_locator import inset_axes

生成一些随机变量，并计算一系列 lmbda 值的 Yeo-Johnson 对数似然值

>>> x = stats.loggamma.rvs(5, loc=10, size=1000)
>>> lmbdas = np.linspace(-2, 10)
>>> llf = np.zeros(lmbdas.shape, dtype=float)
>>> for ii, lmbda in enumerate(lmbdas):
...     llf[ii] = stats.yeojohnson_llf(lmbda, x)

同时使用 yeojohnson 找到最佳 lmbda 值

>>> x_most_normal, lmbda_optimal = stats.yeojohnson(x)

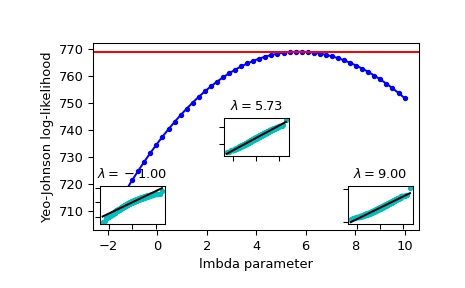
绘制对数似然作为 lmbda 的函数。 添加最佳 lmbda 作为水平线，以检查这是否真的是最优值

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(lmbdas, llf, 'b.-')
>>> ax.axhline(stats.yeojohnson_llf(lmbda_optimal, x), color='r')
>>> ax.set_xlabel('lmbda parameter')
>>> ax.set_ylabel('Yeo-Johnson log-likelihood')

现在添加一些概率图，以显示在对数似然最大化的地方，用 yeojohnson 变换的数据看起来最接近正态分布

>>> locs = [3, 10, 4]  # 'lower left', 'center', 'lower right'
>>> for lmbda, loc in zip([-1, lmbda_optimal, 9], locs):
...     xt = stats.yeojohnson(x, lmbda=lmbda)
...     (osm, osr), (slope, intercept, r_sq) = stats.probplot(xt)
...     ax_inset = inset_axes(ax, width="20%", height="20%", loc=loc)
...     ax_inset.plot(osm, osr, 'c.', osm, slope*osm + intercept, 'k-')
...     ax_inset.set_xticklabels([])
...     ax_inset.set_yticklabels([])
...     ax_inset.set_title(r'$\lambda=%1.2f$' % lmbda)

>>> plt.show()

返回在新标签页中打开