Ctrl+K

scipy.stats.normal_inverse_gamma#

scipy.stats.normal_inverse_gamma = <scipy.stats._multivariate.normal_inverse_gamma_gen object>[源代码]#

正态-逆伽马分布。

正态-逆伽马分布是具有未知均值和方差的正态分布的共轭先验。

参数:
mu, lmbda, a, barray_like

分布的形状参数。请参阅注释。

seed{None, int, np.random.RandomState, np.random.Generator}, 可选

用于绘制随机变量。如果 seed 为 None，则使用 RandomState 单例。如果 seed 是一个整数，则使用一个新的 RandomState 实例，并使用 seed 进行种子设定。如果 seed 已经是 RandomState 或 Generator 实例，则使用该对象。默认为 None。

另请参阅

norm
invgamma

注释

normal_inverse_gamma 的概率密度函数为

\[f(x, \sigma^2; \mu, \lambda, \alpha, \beta) = \frac{\sqrt{\lambda}}{\sqrt{2 \pi \sigma^2}} \frac{\beta^\alpha}{\Gamma(\alpha)} \left( \frac{1}{\sigma^2} \right)^{\alpha + 1} \exp \left(- \frac{2 \beta + \lambda (x - \mu)^2} {2 \sigma^2} \right)\]

其中所有参数均为实数且有限，且 \(\sigma^2 > 0\), \(\lambda > 0\), \(\alpha > 0\), 和 \(\beta > 0\)。

方法 normal_inverse_gamma.pdf 和 normal_inverse_gamma.logpdf 接受 x 和 s2 作为参数 \(x\) 和 \(\sigma^2\)。所有方法都接受 mu, lmbda, a, 和 b 作为形状参数 \(\mu\), \(\lambda\), \(\alpha\), 和 \(\beta\)。

在 1.15 版本中添加。

参考资料

[1]

正态-逆伽马分布，维基百科，https://en.wikipedia.org/wiki/Normal-inverse-gamma_distribution

示例

假设我们希望研究正态-逆伽马分布和逆伽马分布之间的关系。

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> mu, lmbda, a, b = 0, 1, 20, 20
>>> norm_inv_gamma = stats.normal_inverse_gamma(mu, lmbda, a, b)
>>> inv_gamma = stats.invgamma(a, scale=b)

一种方法是将随机变量的 s2 元素的分布与逆伽马分布的 PDF 进行比较。

>>> _, s2 = norm_inv_gamma.rvs(size=10000, random_state=rng)
>>> bins = np.linspace(s2.min(), s2.max(), 50)
>>> plt.hist(s2, bins=bins, density=True, label='Frequency density')
>>> s2 = np.linspace(s2.min(), s2.max(), 300)
>>> plt.plot(s2, inv_gamma.pdf(s2), label='PDF')
>>> plt.xlabel(r'$\sigma^2$')
>>> plt.ylabel('Frequency density / PMF')
>>> plt.show()
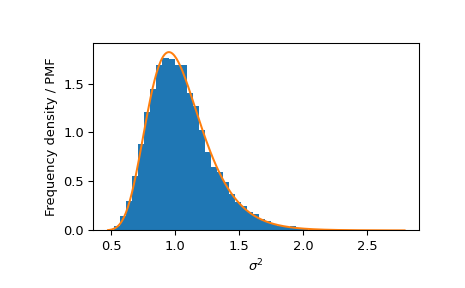
../../_images/scipy-stats-normal_inverse_gamma-1_00_00.png

类似地，我们可以将 s2 的边际分布与逆伽马分布进行比较。

>>> from scipy.integrate import quad_vec
>>> from scipy import integrate
>>> s2 = np.linspace(0.5, 3, 6)
>>> res = quad_vec(lambda x: norm_inv_gamma.pdf(x, s2), -np.inf, np.inf)[0]
>>> np.allclose(res, inv_gamma.pdf(s2))
True

样本均值与分布的均值相当。

>>> x, s2 = norm_inv_gamma.rvs(size=10000, random_state=rng)
>>> x.mean(), s2.mean()
(np.float64(-0.005254750127304425), np.float64(1.050438111436508))
>>> norm_inv_gamma.mean()
(np.float64(0.0), np.float64(1.0526315789473684))

类似地，对于方差

>>> x.var(ddof=1), s2.var(ddof=1)
(np.float64(1.0546150578185023), np.float64(0.061829865266330754))
>>> norm_inv_gamma.var()
(np.float64(1.0526315789473684), np.float64(0.061557402277623886))

方法

pdf(x, s2, mu=0, lmbda=1, a=1, b=1)

概率密度函数。

logpdf(x, s2, mu=0, lmbda=1, a=1, b=1)

概率密度函数的对数。

mean(mu=0, lmbda=1, a=1, b=1)

分布均值。

var(mu=0, lmbda=1, a=1, b=1)

分布方差。

rvs(mu=0, lmbda=1, a=1, b=1, size=None, random_state=None)

绘制随机样本。
在本页