scipy.special.gamma#

scipy.special.gamma(z, out=None) = <ufunc 'gamma'>#

伽马函数。

伽马函数定义为

\[\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt\]

对于 \(\Re(z) > 0\)，并通过解析延拓扩展到复平面的其余部分。更多详情请参阅 [dlmf]。

参数:

zarray_like: 实数或复数值参数
outndarray, 可选: 可选的函数值输出数组

返回:

标量或 ndarray: 伽马函数的值

说明

伽马函数常被称为广义阶乘，因为对于自然数 \(\Gamma(n + 1) = n!\)。更一般地，对于复数 \(z\)，它满足递推关系 \(\Gamma(z + 1) = z \cdot \Gamma(z)\)，这与 \(\Gamma(1) = 1\) 的事实相结合，意味着当 \(z = n\) 时上述恒等式成立。

伽马函数在非负整数处有极点，当 z 接近每个极点时，无穷大的符号取决于接近极点的方向。因此，一致的做法是让 gamma(z) 在负整数处返回 NaN，当 x = -0.0 时返回 -inf，当 x = 0.0 时返回 +inf，使用零的符号位来表示接近原点的方向。例如，这是 Iso C 99 标准 [isoc99] 附录 F 第 9.5.4 条中对伽马函数的建议。

在 SciPy 1.15 版本之前，scipy.special.gamma(z) 在每个极点处返回 +inf。这在 1.15 版本中得到了修复，但带来了以下后果。当伽马函数出现在分母中的表达式，例如

gamma(u) * gamma(v) / (gamma(w) * gamma(x))

如果分子定义良好但分母存在极点，则不再计算为 0。相反，此类表达式会计算为 NaN。在这种情况下，我们建议改用函数 rgamma 来表示倒数伽马函数。上述表达式例如可以写为

gamma(u) * gamma(v) * (rgamma(w) * rgamma(x))

参考文献

[dlmf]

NIST 数学函数数字库 https://dlmf.nist.gov/5.2#E1

[isoc99]

https://www.open-std.org/jtc1/sc22/wg14/www/docs/n1256.pdf

示例

>>> import numpy as np
>>> from scipy.special import gamma, factorial

>>> gamma([0, 0.5, 1, 5])
array([         inf,   1.77245385,   1.        ,  24.        ])

>>> z = 2.5 + 1j
>>> gamma(z)
(0.77476210455108352+0.70763120437959293j)
>>> gamma(z+1), z*gamma(z)  # Recurrence property
((1.2292740569981171+2.5438401155000685j),
 (1.2292740569981158+2.5438401155000658j))

>>> gamma(0.5)**2  # gamma(0.5) = sqrt(pi)
3.1415926535897927

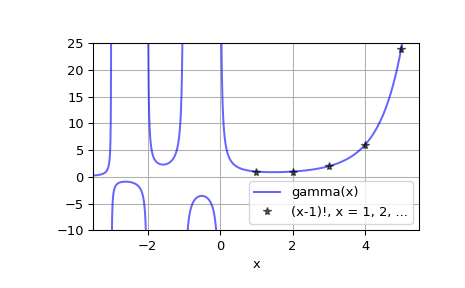
绘制实数 x 的 gamma(x)

>>> x = np.linspace(-3.5, 5.5, 2251)
>>> y = gamma(x)

>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'b', alpha=0.6, label='gamma(x)')
>>> k = np.arange(1, 7)
>>> plt.plot(k, factorial(k-1), 'k*', alpha=0.6,
...          label='(x-1)!, x = 1, 2, ...')
>>> plt.xlim(-3.5, 5.5)
>>> plt.ylim(-10, 25)
>>> plt.grid()
>>> plt.xlabel('x')
>>> plt.legend(loc='lower right')
>>> plt.show()