scipy.special.pseudo_huber#
- scipy.special.pseudo_huber(delta, r, out=None) = <ufunc 'pseudo_huber'>#
Pseudo-Huber 损失函数。
\[\mathrm{pseudo\_huber}(\delta, r) = \delta^2 \left( \sqrt{ 1 + \left( \frac{r}{\delta} \right)^2 } - 1 \right)\]- 参数:
- deltaarray_like
输入数组,指示软二次损失与线性损失的转折点。
- rarray_like
输入数组,可能表示残差。
- outndarray,可选
函数结果的可选输出数组
- 返回:
- res标量或 ndarray
计算的 Pseudo-Huber 损失函数值。
参见
huber与此函数近似的相似函数
备注
与
huber一样,pseudo_huber通常用作统计或机器学习中的鲁棒损失函数,以减少异常值的影响。 与huber不同,pseudo_huber是平滑的。通常,r 表示残差,即模型预测和数据之间的差异。 然后,对于 \(|r|\leq\delta\),
pseudo_huber类似于平方误差,对于 \(|r|>\delta\),则类似于绝对误差。 这样,Pseudo-Huber 损失通常可以在模型拟合中针对小残差实现快速收敛,如平方误差损失函数一样,并且仍然可以减少异常值的影响(\(|r|>\delta\)),如绝对误差损失一样。 由于 \(\delta\) 是平方误差和绝对误差状态之间的截止值,因此必须针对每个问题仔细调整。pseudo_huber也是凸的,使其适合基于梯度的优化。 [1] [2]0.15.0 版本新增。
参考文献
[1]Hartley, Zisserman, “计算机视觉中的多视图几何”。 2003. 剑桥大学出版社。 第 619 页
[2]Charbonnier et al. “计算机成像中的确定性边缘保留正则化”。 1997. IEEE Trans. 图像处理。 6 (2): 298 - 311。
示例
导入所有必要的模块。
>>> import numpy as np >>> from scipy.special import pseudo_huber, huber >>> import matplotlib.pyplot as plt
在
r=2处计算delta=1的函数。>>> pseudo_huber(1., 2.) 1.2360679774997898
通过为 delta 提供列表或 NumPy 数组,计算
r=2处不同 delta 的函数。>>> pseudo_huber([1., 2., 4.], 3.) array([2.16227766, 3.21110255, 4. ])
通过为 r 提供列表或 NumPy 数组,计算
delta=1处多个点的函数。>>> pseudo_huber(2., np.array([1., 1.5, 3., 4.])) array([0.47213595, 1. , 3.21110255, 4.94427191])
可以通过为 delta 和 r 都提供具有兼容广播形状的数组来计算该函数。
>>> r = np.array([1., 2.5, 8., 10.]) >>> deltas = np.array([[1.], [5.], [9.]]) >>> print(r.shape, deltas.shape) (4,) (3, 1)
>>> pseudo_huber(deltas, r) array([[ 0.41421356, 1.6925824 , 7.06225775, 9.04987562], [ 0.49509757, 2.95084972, 22.16990566, 30.90169944], [ 0.49846624, 3.06693762, 27.37435121, 40.08261642]])
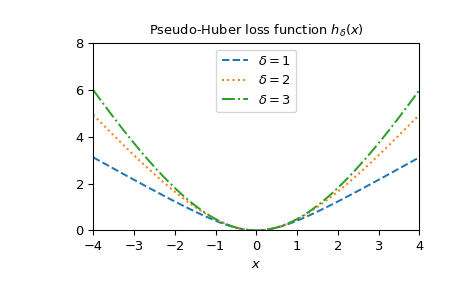
绘制不同 delta 的函数。
>>> x = np.linspace(-4, 4, 500) >>> deltas = [1, 2, 3] >>> linestyles = ["dashed", "dotted", "dashdot"] >>> fig, ax = plt.subplots() >>> combined_plot_parameters = list(zip(deltas, linestyles)) >>> for delta, style in combined_plot_parameters: ... ax.plot(x, pseudo_huber(delta, x), label=rf"$\delta={delta}$", ... ls=style) >>> ax.legend(loc="upper center") >>> ax.set_xlabel("$x$") >>> ax.set_title(r"Pseudo-Huber loss function $h_{\delta}(x)$") >>> ax.set_xlim(-4, 4) >>> ax.set_ylim(0, 8) >>> plt.show()
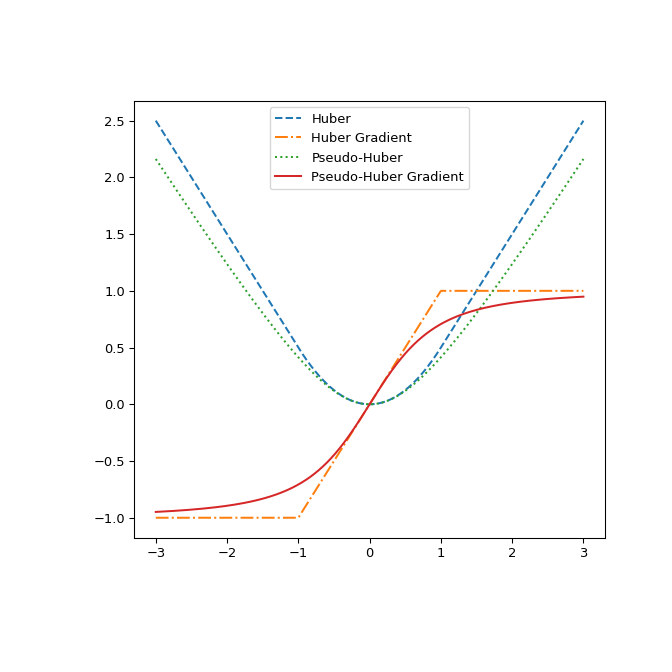
最后,通过绘制它们及其相对于 r 的梯度来展示
huber和pseudo_huber之间的差异。 该图显示pseudo_huber是连续可微的,而huber在点 \(\pm\delta\) 处不可微。>>> def huber_grad(delta, x): ... grad = np.copy(x) ... linear_area = np.argwhere(np.abs(x) > delta) ... grad[linear_area]=delta*np.sign(x[linear_area]) ... return grad >>> def pseudo_huber_grad(delta, x): ... return x* (1+(x/delta)**2)**(-0.5) >>> x=np.linspace(-3, 3, 500) >>> delta = 1. >>> fig, ax = plt.subplots(figsize=(7, 7)) >>> ax.plot(x, huber(delta, x), label="Huber", ls="dashed") >>> ax.plot(x, huber_grad(delta, x), label="Huber Gradient", ls="dashdot") >>> ax.plot(x, pseudo_huber(delta, x), label="Pseudo-Huber", ls="dotted") >>> ax.plot(x, pseudo_huber_grad(delta, x), label="Pseudo-Huber Gradient", ... ls="solid") >>> ax.legend(loc="upper center") >>> plt.show()