scipy.special.huber#

scipy.special.huber(delta, r, out=None) = <ufunc 'huber'>#

Huber 损失函数。

\[\begin{split}\text{huber}(\delta, r) = \begin{cases} \infty & \delta < 0 \\ \frac{1}{2}r^2 & 0 \le \delta, | r | \le \delta \\ \delta ( |r| - \frac{1}{2}\delta ) & \text{otherwise} \end{cases}\end{split}\]

参数:

deltandarray: 输入数组，表示二次与线性损失的转折点。
rndarray: 输入数组，可能表示残差。
outndarray, optional: 用于存储函数值的可选输出数组

返回:

标量或 ndarray: 计算出的 Huber 损失函数值。

另请参阅

pseudo_huber: 该函数的平滑近似

备注

huber 在鲁棒统计或机器学习中作为损失函数非常有用，它与常见的平方误差损失相比，可以减少异常值的影响，即幅度高于 delta 的残差不进行平方处理 [1]。

通常，r 表示残差，即模型预测与数据之间的差异。那么，对于 \(|r|\leq\delta\)，huber 类似于平方误差；对于 \(|r|>\delta\)，则类似于绝对误差。通过这种方式，Huber 损失在模型拟合中通常可以像平方误差损失函数一样对小残差实现快速收敛，并且仍然可以像绝对误差损失一样减少异常值（\(|r|>\delta\)）的影响。由于 \(\delta\) 是平方误差和绝对误差区域之间的截止点，因此需要针对每个问题仔细调整。huber 也是凸函数，因此适用于基于梯度的优化。

在 0.15.0 版中新增。

参考

[1]

Peter Huber. “Robust Estimation of a Location Parameter”, 1964. Annals of Statistics. 53 (1): 73 - 101.

示例

导入所有必要的模块。

>>> import numpy as np
>>> from scipy.special import huber
>>> import matplotlib.pyplot as plt

计算 delta=1 且 r=2 时的函数值

>>> huber(1., 2.)
1.5

通过为 delta 提供 NumPy 数组或列表来计算不同 delta 时的函数值。

>>> huber([1., 3., 5.], 4.)
array([3.5, 7.5, 8. ])

通过为 r 提供 NumPy 数组或列表来计算不同点上的函数值。

>>> huber(2., np.array([1., 1.5, 3.]))
array([0.5  , 1.125, 4.   ])

通过为 delta 和 r 提供具有兼容广播形状的数组，可以计算不同 delta 和 r 时的函数值。

>>> r = np.array([1., 2.5, 8., 10.])
>>> deltas = np.array([[1.], [5.], [9.]])
>>> print(r.shape, deltas.shape)
(4,) (3, 1)

>>> huber(deltas, r)
array([[ 0.5  ,  2.   ,  7.5  ,  9.5  ],
       [ 0.5  ,  3.125, 27.5  , 37.5  ],
       [ 0.5  ,  3.125, 32.   , 49.5  ]])

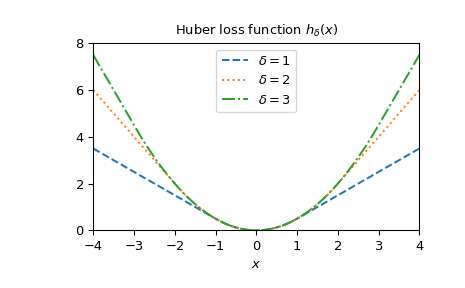
绘制不同 delta 时的函数。

>>> x = np.linspace(-4, 4, 500)
>>> deltas = [1, 2, 3]
>>> linestyles = ["dashed", "dotted", "dashdot"]
>>> fig, ax = plt.subplots()
>>> combined_plot_parameters = list(zip(deltas, linestyles))
>>> for delta, style in combined_plot_parameters:
...     ax.plot(x, huber(delta, x), label=fr"$\delta={delta}$", ls=style)
>>> ax.legend(loc="upper center")
>>> ax.set_xlabel("$x$")
>>> ax.set_title(r"Huber loss function $h_{\delta}(x)$")
>>> ax.set_xlim(-4, 4)
>>> ax.set_ylim(0, 8)
>>> plt.show()