scipy.signal.

freqz_zpk#

scipy.signal.freqz_zpk(z, p, k, worN=512, whole=False, fs=6.283185307179586)[源码]#

计算ZPK形式的数字滤波器的频率响应。

给定数字滤波器的零点、极点和增益，计算其频率响应

\(H(z)=k \prod_i (z - Z[i]) / \prod_j (z - P[j])\)

其中 \(k\) 是增益，\(Z\) 是零点，\(P\) 是极点。

参数:

zarray_like

线性滤波器的零点

parray_like

线性滤波器的极点

k标量

线性滤波器的增益

worN{None, int, array_like}，可选

如果是一个整数，则在该数量的频率点上计算（默认为N=512）。

如果是一个类数组，则在给定频率点上计算响应。这些频率的单位与fs相同。

whole布尔值，可选

通常，频率计算范围是从0到奈奎斯特频率fs/2（单位圆的上半部分）。如果whole为True，则计算频率范围是从0到fs。如果w是类数组，则忽略此参数。

fs浮点数，可选

数字系统的采样频率。默认为2*pi弧度/样本（因此w的范围是从0到pi）。

在版本1.2.0中新增。

返回:

wndarray: 计算h时的频率，单位与fs相同。默认情况下，w被归一化到范围[0, pi)（弧度/样本）。
hndarray: 频率响应，以复数形式表示。

另请参阅

freqs: 计算TF形式的模拟滤波器的频率响应
freqs_zpk: 计算ZPK形式的模拟滤波器的频率响应
freqz: 计算TF形式的数字滤波器的频率响应

备注

在版本0.19.0中新增。

示例

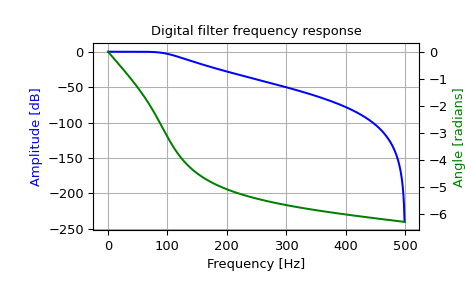
设计一个4阶数字巴特沃斯滤波器，在采样率为1000 Hz的系统中，截止频率为100 Hz，并绘制其频率响应

>>> import numpy as np
>>> from scipy import signal
>>> z, p, k = signal.butter(4, 100, output='zpk', fs=1000)
>>> w, h = signal.freqz_zpk(z, p, k, fs=1000)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 1, 1)
>>> ax1.set_title('Digital filter frequency response')

>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [Hz]')
>>> ax1.grid(True)

>>> ax2 = ax1.twinx()
>>> phase = np.unwrap(np.angle(h))
>>> ax2.plot(w, phase, 'g')
>>> ax2.set_ylabel('Phase [rad]', color='g')

>>> plt.axis('tight')
>>> plt.show()

../../_images/scipy-signal-freqz_zpk-1.png