scipy.signal.

firls#

scipy.signal.firls(numtaps, bands, desired, *, weight=None, fs=None)[源代码]#

使用最小二乘误差最小化设计 FIR 滤波器。

计算线性相位有限脉冲响应（FIR）滤波器的系数，该滤波器在最小二乘意义上对由 bands 和 desired 描述的期望频率响应具有最佳逼近（即，最小化指定频带内加权均方误差的积分）。

参数:

numtapsint: FIR 滤波器中的抽头数量。numtaps 必须是奇数。
bandsarray_like: 一个单调非递减序列，包含以赫兹为单位的频带边缘。所有元素必须是非负的，并且小于或等于由 nyq 给出的奈奎斯特频率。频带指定为频率对，因此，如果使用一维数组，其长度必须是偶数，例如 np.array([0, 1, 2, 3, 4, 5])。或者，频带可以指定为一个 nx2 大小的二维数组，其中 n 是频带的数量，例如 np.array([[0, 1], [2, 3], [4, 5]])。
desiredarray_like: 一个与 bands 大小相同的序列，包含每个频带起点和终点处的期望增益。
weightarray_like, optional: 在解决最小二乘问题时，赋予每个频带区域的相对权重。weight 的大小必须是 bands 的一半。
fsfloat, optional: 信号的采样频率。bands 中的每个频率必须在 0 到 fs/2 之间（包括）。默认值为 2。

返回:

coeffsndarray: 最优（最小二乘意义上）FIR 滤波器的系数。

另请参阅

firwin
firwin2
minimum_phase
remez

备注

此实现遵循了 [1] 中给出的算法。如该处所述，最小二乘设计具有多重优点

在最小二乘意义上是最佳的。

简单、非迭代的方法。

可以通过求解线性方程组获得通用解。

允许使用依赖于频率的加权函数。

此函数构建了一个 I 型线性相位 FIR 滤波器，它包含奇数个 coeffs，满足 \(n < numtaps\)

\[coeffs(n) = coeffs(numtaps - 1 - n)\]

奇数个系数和滤波器对称性避免了在奈奎斯特频率和 0 频率处可能出现的边界条件（例如，对于 II 型、III 型或 IV 型变体）。

在 0.18 版本中新增。

参考文献

[1]

Ivan Selesnick, Linear-Phase Fir Filter Design By Least Squares. OpenStax CNX. Aug 9, 2005. https://eeweb.engineering.nyu.edu/iselesni/EL713/firls/firls.pdf

示例

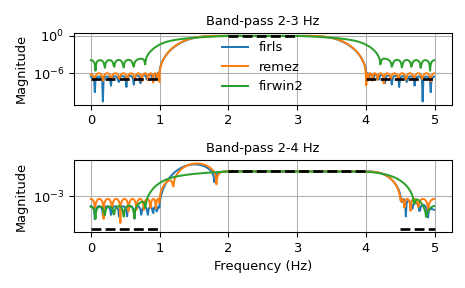
我们想要构建一个带通滤波器。请注意，在阻带和通带之间的频率范围内的行为是未指定的，因此可能会根据我们滤波器的参数而出现过冲。

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> fig, axs = plt.subplots(2)
>>> fs = 10.0  # Hz
>>> desired = (0, 0, 1, 1, 0, 0)
>>> for bi, bands in enumerate(((0, 1, 2, 3, 4, 5), (0, 1, 2, 4, 4.5, 5))):
...     fir_firls = signal.firls(73, bands, desired, fs=fs)
...     fir_remez = signal.remez(73, bands, desired[::2], fs=fs)
...     fir_firwin2 = signal.firwin2(73, bands, desired, fs=fs)
...     hs = list()
...     ax = axs[bi]
...     for fir in (fir_firls, fir_remez, fir_firwin2):
...         freq, response = signal.freqz(fir)
...         hs.append(ax.semilogy(0.5*fs*freq/np.pi, np.abs(response))[0])
...     for band, gains in zip(zip(bands[::2], bands[1::2]),
...                            zip(desired[::2], desired[1::2])):
...         ax.semilogy(band, np.maximum(gains, 1e-7), 'k--', linewidth=2)
...     if bi == 0:
...         ax.legend(hs, ('firls', 'remez', 'firwin2'),
...                   loc='lower center', frameon=False)
...     else:
...         ax.set_xlabel('Frequency (Hz)')
...     ax.grid(True)
...     ax.set(title='Band-pass %d-%d Hz' % bands[2:4], ylabel='Magnitude')
...
>>> fig.tight_layout()
>>> plt.show()