scipy.signal.

find_peaks#

scipy.signal.find_peaks(x, height=None, threshold=None, distance=None, prominence=None, width=None, wlen=None, rel_height=0.5, plateau_size=None)[source]#

根据峰值属性查找信号中的峰值。

此函数接受一个一维数组，并通过简单比较相邻值来查找所有局部最大值。可选地，可以通过为峰值属性指定条件来选择这些峰值的一个子集。

参数:
xsequence

带有峰值的信号。

height数字或 ndarray 或序列，可选

所需的峰值高度。可以是数字、None、与 x 匹配的数组或前者的2元素序列。第一个元素始终被解释为最小所需高度，如果提供第二个元素，则解释为最大所需高度。

threshold数字或 ndarray 或序列，可选

所需的峰值阈值，即其与相邻样本的垂直距离。可以是数字、None、与 x 匹配的数组或前者的2元素序列。第一个元素始终被解释为最小所需阈值，如果提供第二个元素，则解释为最大所需阈值。

distance数字，可选

相邻峰值之间所需的最小水平距离（>= 1）以样本为单位。较小的峰值首先被移除，直到所有剩余峰值都满足条件。

prominence数字或 ndarray 或序列，可选

所需的峰值显著性。可以是数字、None、与 x 匹配的数组或前者的2元素序列。第一个元素始终被解释为最小所需显著性，如果提供第二个元素，则解释为最大所需显著性。

width数字或 ndarray 或序列，可选

所需的峰值宽度，以样本为单位。可以是数字、None、与 x 匹配的数组或前者的2元素序列。第一个元素始终被解释为最小所需宽度，如果提供第二个元素，则解释为最大所需宽度。

wlen整数，可选

用于计算峰值显著性，因此仅当给出 prominence 或 width 参数之一时才使用。有关其效果的完整描述，请参阅 peak_prominences 中的参数 wlen。

rel_height浮点数，可选

用于计算峰值宽度，因此仅当给出 width 时才使用。有关其效果的完整描述，请参阅 peak_widths 中的参数 rel_height。

plateau_size数字或 ndarray 或序列，可选

所需的峰值平顶大小，以样本为单位。可以是数字、None、与 x 匹配的数组或前者的2元素序列。第一个元素始终被解释为最小所需平顶大小，如果提供第二个元素，则解释为最大所需平顶大小。

在 1.2.0 版中新增。

返回:
peaksndarray

满足所有给定条件的 x 中峰值的索引。

propertiesdict

一个字典，包含返回峰值的属性，这些属性是在评估指定条件期间作为中间结果计算的。

  • ‘peak_heights’

    如果给定 height，则为 x 中每个峰值的高度。

  • ‘left_thresholds’, ‘right_thresholds’

    如果给定 threshold，这些键包含峰值与其相邻样本的垂直距离。

  • ‘prominences’, ‘right_bases’, ‘left_bases’

    如果给定 prominence，这些键可访问。有关其内容的描述，请参阅 peak_prominences。

  • ‘widths’, ‘width_heights’, ‘left_ips’, ‘right_ips’

    如果给定 width，这些键可访问。有关其内容的描述，请参阅 peak_widths。

  • ‘plateau_sizes’, left_edges’, ‘right_edges’

    如果给定 plateau_size，这些键可访问，并包含峰值边缘的索引（边缘仍是平顶的一部分）以及计算出的平顶大小。

    在 1.2.0 版中新增。

要在不排除峰值的情况下计算并返回属性，请将开放区间 (None, None) 作为值提供给相应参数（不包括 distance）。

警告:
PeakPropertyWarning

如果峰值属性具有意外值，则引发此警告（请参阅 peak_prominences 和 peak_widths）。

警告

此函数对于包含 NaNs 的数据可能会返回意外结果。为避免这种情况，应删除或替换 NaNs。

另请参阅

find_peaks_cwt

使用小波变换查找峰值。

peak_prominences

直接计算峰值的显著性。

peak_widths

直接计算峰值的宽度。

注释

在此函数的上下文中，峰值或局部最大值定义为任何两个直接邻居具有较小幅度的样本。对于平坦峰值（一个或多个具有相同幅度的样本），返回中间样本的索引（如果样本数量为偶数，则向下取整）。对于噪声信号，峰值位置可能会偏离，因为噪声可能会改变局部最大值的位置。在这些情况下，请考虑在查找峰值之前对信号进行平滑处理，或使用其他峰值查找和拟合方法（如 find_peaks_cwt）。

关于指定条件的一些补充注释

  • 几乎所有条件（不包括 distance）都可以表示为半开区间或闭合区间，例如，1 或 (1, None) 定义半开区间 \([1, \infty]\)，而 (None, 1) 定义区间 \([-\infty, 1]\)。也可以指定开放区间 (None, None)，这将返回匹配的属性而不排除峰值。

  • 边界始终包含在用于选择有效峰值的区间内。

  • 对于某些条件，区间边界可以用与 x 形状匹配的数组指定，这使得可以根据样本位置进行动态约束。

  • 条件按以下顺序评估：plateau_size、height、threshold、distance、prominence、width。在大多数情况下，这个顺序是最快的，因为更快的操作会首先应用，以减少稍后需要评估的峰值数量。

  • 虽然 peaks 中的索引保证至少相距 distance 个样本，但平坦峰值的边缘可能比允许的 distance 更近。

  • 如果 x 很大或有许多局部最大值，请使用 wlen 来减少评估 prominence 或 width 条件所需的时间（请参阅 peak_prominences）。

在 1.1.0 版中新增。

示例

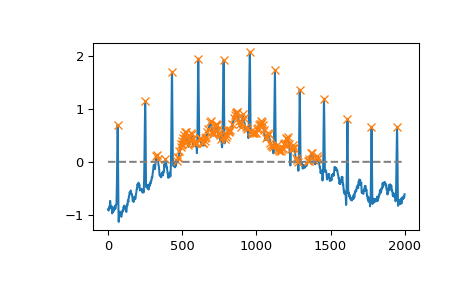
为了演示此函数的使用，我们使用 SciPy 提供的信号 x（请参阅 scipy.datasets.electrocardiogram）。让我们找出 x 中幅度大于 0 的所有峰值（局部最大值）。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.datasets import electrocardiogram
>>> from scipy.signal import find_peaks
>>> x = electrocardiogram()[2000:4000]
>>> peaks, _ = find_peaks(x, height=0)
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.plot(np.zeros_like(x), "--", color="gray")
>>> plt.show()
../../_images/scipy-signal-find_peaks-1_00_00.png

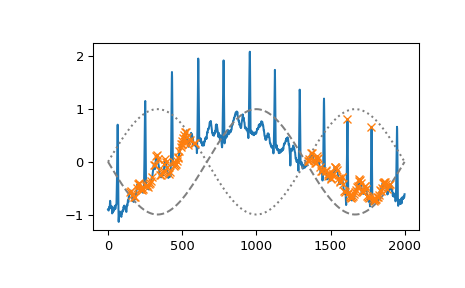
我们可以使用 height=(None, 0) 选择小于 0 的峰值，或使用与 x 大小匹配的数组来反映信号不同部分的动态条件。

>>> border = np.sin(np.linspace(0, 3 * np.pi, x.size))
>>> peaks, _ = find_peaks(x, height=(-border, border))
>>> plt.plot(x)
>>> plt.plot(-border, "--", color="gray")
>>> plt.plot(border, ":", color="gray")
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.show()
../../_images/scipy-signal-find_peaks-1_01_00.png

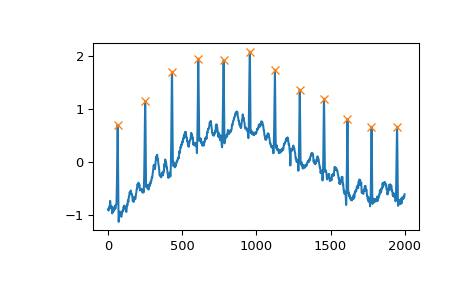
对于周期性信号，可以使用 distance 参数给出另一个有用的条件。在这种情况下，我们可以通过要求至少 150 个样本的距离，轻松选择心电图 (ECG) 中 QRS 波群的位置。

>>> peaks, _ = find_peaks(x, distance=150)
>>> np.diff(peaks)
array([186, 180, 177, 171, 177, 169, 167, 164, 158, 162, 172])
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.show()
../../_images/scipy-signal-find_peaks-1_02_00.png

特别是对于噪声信号，可以通过峰值显著性轻松对峰值进行分组（请参阅 peak_prominences）。例如，我们可以通过将允许的显著性限制为 0.6 来选择除所述 QRS 波群之外的所有峰值。

>>> peaks, properties = find_peaks(x, prominence=(None, 0.6))
>>> properties["prominences"].max()
0.5049999999999999
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.show()
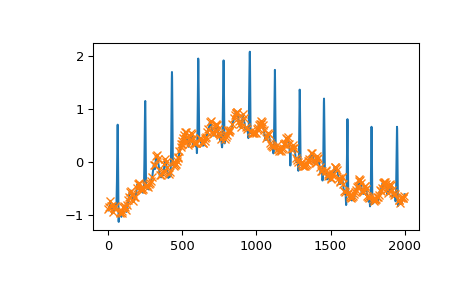
../../_images/scipy-signal-find_peaks-1_03_00.png

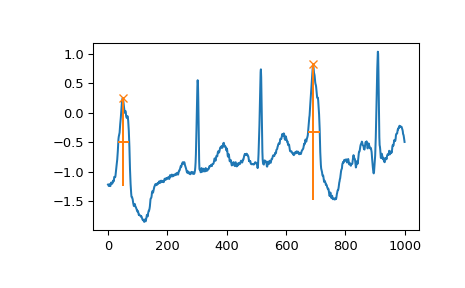
最后，让我们检查一下 ECG 的另一个部分，其中包含不同形状的心跳。为了只选择非典型心跳，我们结合了两个条件：最小显著性为 1，宽度至少为 20 个样本。

>>> x = electrocardiogram()[17000:18000]
>>> peaks, properties = find_peaks(x, prominence=1, width=20)
>>> properties["prominences"], properties["widths"]
(array([1.495, 2.3  ]), array([36.93773946, 39.32723577]))
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.vlines(x=peaks, ymin=x[peaks] - properties["prominences"],
...            ymax = x[peaks], color = "C1")
>>> plt.hlines(y=properties["width_heights"], xmin=properties["left_ips"],
...            xmax=properties["right_ips"], color = "C1")
>>> plt.show()
../../_images/scipy-signal-find_peaks-1_04_00.png
本页内容