scipy.signal.

peak_prominences#

scipy.signal.peak_prominences(x, peaks, wlen=None)[源代码]#

计算信号中每个峰值的显著性。

峰值的显著性衡量了峰值从信号周围基线中突出多少，定义为峰值与其最低等高线之间的垂直距离。

参数:
x序列

带有峰值的信号。

peaks序列

x 中峰值的索引。

wlen整数, 可选

以采样点为单位的窗口长度，可选地将每个峰值的评估区域限制为 x 的子集。峰值始终位于窗口的中间，因此给定长度会向上舍入到下一个奇数整数。此参数可以加快计算速度（参见注意事项）。

返回:
prominencesndarray

为 peaks 中的每个峰值计算的显著性。

left_bases, right_basesndarray

峰值的基点，作为 x 中每个峰值左右两侧的索引。每对基点中较高的一个是峰值的最低等高线。

引发:
ValueError

如果 peaks 中的某个值是 x 的无效索引。

警告:
PeakPropertyWarning

对于 peaks 中不指向 x 中有效局部最大值的索引，返回的显著性将为 0 并引发此警告。如果 wlen 小于峰值的平台大小，也会发生这种情况。

警告

此函数对于包含 NaNs 的数据可能会返回意外结果。为避免这种情况，应移除或替换 NaNs。

另请参阅

find_peaks

根据峰值属性在信号中查找峰值。

peak_widths

计算峰值的宽度。

注意事项

计算峰值显著性的策略

  1. 从当前峰值向左和向右延伸一条水平线，直到该线到达窗口边界（参见 wlen）或在更高峰值的斜坡处再次与信号相交。与相同高度的峰值相交的情况将被忽略。

  2. 在每一侧，找到上述定义区间内的最小信号值。这些点是峰值的基点。

  3. 两个基点中较高的一个标志着峰值的最低等高线。显著性可以计算为峰值自身高度与其最低等高线之间的垂直差异。

对于具有周期性行为的大型 x，搜索峰值的基点可能很慢，因为第一个算法步骤需要评估大块甚至整个信号。这个评估区域可以通过参数 wlen 来限制，它将算法限制在当前峰值周围的一个窗口内，并且如果窗口长度相对于 x 较短，可以缩短计算时间。然而，如果峰值的真实基点在此窗口之外，这可能会阻止算法找到真正的全局等高线。相反，在受限窗口内会找到更高的等高线，导致计算出的显著性更小。实际上，这仅与 x 中最高的一组峰值有关。这种行为甚至可以有意地用于计算“局部”显著性。

在版本 1.1.0 中添加。

参考

[1]

地形显著性维基百科文章: https://en.wikipedia.org/wiki/Topographic_prominence

示例

>>> import numpy as np
>>> from scipy.signal import find_peaks, peak_prominences
>>> import matplotlib.pyplot as plt

创建具有两个叠加谐波的测试信号

>>> x = np.linspace(0, 6 * np.pi, 1000)
>>> x = np.sin(x) + 0.6 * np.sin(2.6 * x)

查找所有峰值并计算显著性

>>> peaks, _ = find_peaks(x)
>>> prominences = peak_prominences(x, peaks)[0]
>>> prominences
array([1.24159486, 0.47840168, 0.28470524, 3.10716793, 0.284603  ,
       0.47822491, 2.48340261, 0.47822491])

计算每个峰值等高线的高度并绘制结果

>>> contour_heights = x[peaks] - prominences
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.vlines(x=peaks, ymin=contour_heights, ymax=x[peaks])
>>> plt.show()
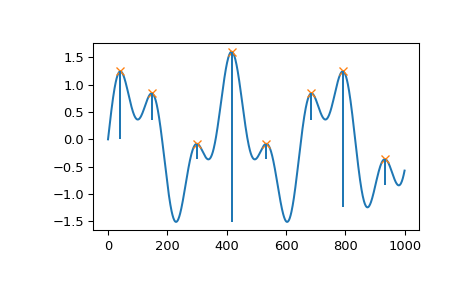
../../_images/scipy-signal-peak_prominences-1_00_00.png

让我们评估第二个示例，该示例演示了索引 5 处一个峰值的几个边缘情况。

>>> x = np.array([0, 1, 0, 3, 1, 3, 0, 4, 0])
>>> peaks = np.array([5])
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.show()
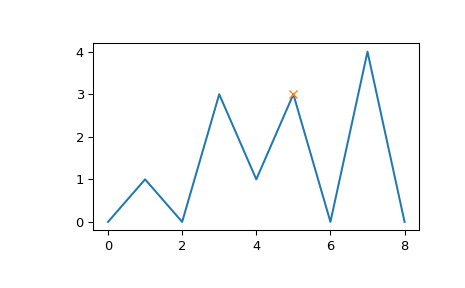
../../_images/scipy-signal-peak_prominences-1_01_00.png 
>>> peak_prominences(x, peaks)  # -> (prominences, left_bases, right_bases)
(array([3.]), array([2]), array([6]))

请注意，在搜索左基点时，索引 3 处相同高度的峰值不被视为边界。相反，在 0 和 2 处找到了两个最小值，在这种情况下，始终选择更接近被评估峰值的那个。然而，在右侧，基点必须放在 6 处，因为更高的峰值代表了评估区域的右边界。

>>> peak_prominences(x, peaks, wlen=3.1)
(array([2.]), array([4]), array([6]))

在这里，我们将算法限制在 3 到 7 的窗口内（长度为 5 个采样点，因为 wlen 向上舍入到下一个奇数整数）。因此，评估区域中仅有的两个候选是两个相邻的采样点，并计算出较小的显著性。

在本页