scipy.interpolate.

Akima1DInterpolator

class scipy.interpolate.Akima1DInterpolator(x, y, axis=0, *, method='akima', extrapolate=None)

Akima “视觉上令人满意”的插值器 (C1 平滑)。

给定向量 x 和 y，拟合分段三次多项式。Akima 插值方法使用由分段三次多项式构建的连续可微子样条。生成的曲线将通过给定数据点，并显得平滑自然。

参数:

xndarray，形状 (npoints, )

单调递增实数值的一维数组。

yndarray，形状 (…, npoints, …)

实数值的 N 维数组。y 沿插值轴的长度必须等于 x 的长度。使用 axis 参数选择插值轴。

axisint，可选

y 数组中与 x 坐标值对应的轴。默认为 axis=0。

method{‘akima’, ‘makima’}，可选

如果为 "makima"，使用修改后的 Akima 插值 [2]。默认为 "akima"，使用 Akima 插值 [1]。

在版本 1.13.0 中新增。

extrapolate{bool, None}，可选

如果为布尔值，则根据第一个和最后一个区间确定是否外推到超出边界的点，或返回 NaNs。如果为 None，extrapolate 将设置为 False。

属性:

axis

c

extrapolate

x

方法

__call__(x[, nu, extrapolate])	评估分段多项式或其导数。
derivative([nu])	构造表示导数的新分段多项式。
antiderivative([nu])	构造表示反导数的新分段多项式。
integrate(a, b[, extrapolate])	计算分段多项式的定积分。
solve([y, discontinuity, extrapolate])	找到方程 pp(x) == y 的实数解。
roots([discontinuity, extrapolate])	找到分段多项式的实数根。

另请参阅

PchipInterpolator

PCHIP 一维单调三次插值器。

CubicSpline

三次样条数据插值器。

PPoly

分段多项式，以系数和断点表示

备注

在版本 0.14 中新增。

仅用于精确数据，因为拟合曲线精确通过给定点。此例程适用于通过少量给定点绘制一条平滑美观的曲线，以供绘图之用。

令 \(\delta_i = (y_{i+1} - y_i) / (x_{i+1} - x_i)\) 为区间 \(\left[x_i, x_{i+1}\right)\) 的斜率。Akima 在 \(x_i\) 处的导数定义为

\[d_i = \frac{w_1}{w_1 + w_2}\delta_{i-1} + \frac{w_2}{w_1 + w_2}\delta_i\]

在 Akima 插值 [1] (method="akima") 中，权重为

\[\begin{split}\begin{aligned} w_1 &= |\delta_{i+1} - \delta_i| \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| \end{aligned}\end{split}\]

在修改后的 Akima 插值 [2] (method="makima") 中，为了消除过冲并避免分子和分母都为 0 的边界情况，权重修改如下

\[\begin{split}\begin{align*} w_1 &= |\delta_{i+1} - \delta_i| + |\delta_{i+1} + \delta_i| / 2 \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| + |\delta_{i-1} + \delta_{i-2}| / 2 \end{align*}\end{split}\]

参考文献

[1] (1,2)

一种基于局部过程的插值和平滑曲线拟合新方法。Hiroshi Akima, J. ACM, 1970年10月, 17(4), 589-602。 DOI:10.1145/321607.321609

[2] (1,2)

Makima 分段三次插值。Cleve Moler 和 Cosmin Ionita, 2019。 https://blogs.mathworks.com/cleve/2019/04/29/makima-piecewise-cubic-interpolation/

示例

在浏览器中尝试！

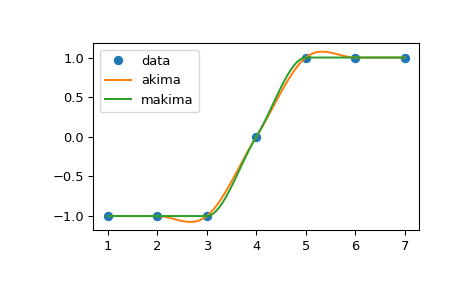
method="akima" 和 method="makima" 的比较

>>> import numpy as np
>>> from scipy.interpolate import Akima1DInterpolator
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(1, 7, 7)
>>> y = np.array([-1, -1, -1, 0, 1, 1, 1])
>>> xs = np.linspace(min(x), max(x), num=100)
>>> y_akima = Akima1DInterpolator(x, y, method="akima")(xs)
>>> y_makima = Akima1DInterpolator(x, y, method="makima")(xs)

>>> fig, ax = plt.subplots()
>>> ax.plot(x, y, "o", label="data")
>>> ax.plot(xs, y_akima, label="akima")
>>> ax.plot(xs, y_makima, label="makima")
>>> ax.legend()
>>> fig.show()

"akima" 中出现的过冲在 "makima" 中已避免。

返回在新标签页中打开