scipy.signal.

czt#

scipy.signal.czt(x, m=None, w=None, a=1 + 0j, *, axis=-1)[source]#

计算 Z 平面中螺旋线周围的频率响应。

参数:

x数组: 要进行变换的信号。
m整数，可选: 所需的输出点数。默认为输入数据的长度。
w复数，可选: 每步中点之间的比率。此参数必须精确，否则累积误差会降低输出序列的尾部。默认为单位圆上等间距的点。
a复数，可选: 复平面中的起始点。默认为 1+0j。
axis整数，可选: 计算 FFT 的轴。如果未指定，则使用最后一个轴。

返回:

outndarray: 一个与 x 具有相同维度但变换轴长度设置为 m 的数组。

另请参阅

CZT: 一个创建可调用线性调频 Z 变换函数的类。
zoom_fft: 用于部分 FFT 计算的便捷函数。

注释

默认值选择如下：signal.czt(x) 等同于 fft.fft(x)；如果 m > len(x)，则 signal.czt(x, m) 等同于 fft.fft(x, m)。

如果需要重复变换，请使用 CZT 构建一个专门的变换函数，该函数可以重复使用而无需重新计算常量。

一个应用示例是在系统辨识中，重复评估系统 Z 变换的小切片（围绕预期存在极点的位置），以精炼对极点真实位置的估计。 [1]

参考文献

[1]

Steve Alan Shilling, “线性调频 Z 变换及其应用研究”, pg 20 (1970) https://krex.k-state.edu/dspace/bitstream/handle/2097/7844/LD2668R41972S43.pdf

示例

生成一个正弦波

>>> import numpy as np
>>> f1, f2, fs = 8, 10, 200  # Hz
>>> t = np.linspace(0, 1, fs, endpoint=False)
>>> x = np.sin(2*np.pi*t*f2)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, x)
>>> plt.axis([0, 1, -1.1, 1.1])
>>> plt.show()

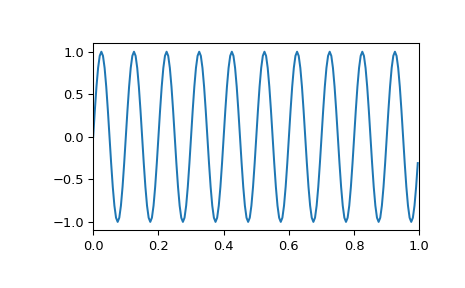
其离散傅里叶变换的所有能量都集中在单个频率 bin 中

>>> from scipy.fft import rfft, rfftfreq
>>> from scipy.signal import czt, czt_points
>>> plt.plot(rfftfreq(fs, 1/fs), abs(rfft(x)))
>>> plt.margins(0, 0.1)
>>> plt.show()

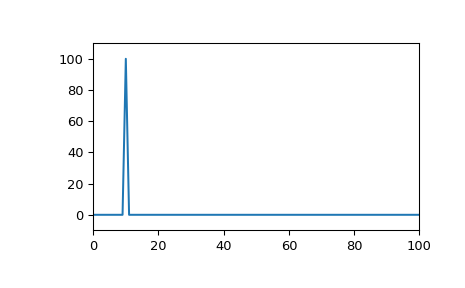
然而，如果正弦波呈对数衰减

>>> x = np.exp(-t*f1) * np.sin(2*np.pi*t*f2)
>>> plt.plot(t, x)
>>> plt.axis([0, 1, -1.1, 1.1])
>>> plt.show()

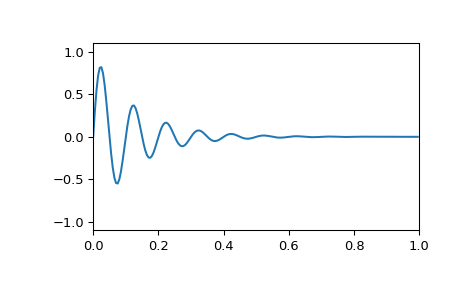
DFT 将出现频谱泄漏

>>> plt.plot(rfftfreq(fs, 1/fs), abs(rfft(x)))
>>> plt.margins(0, 0.1)
>>> plt.show()

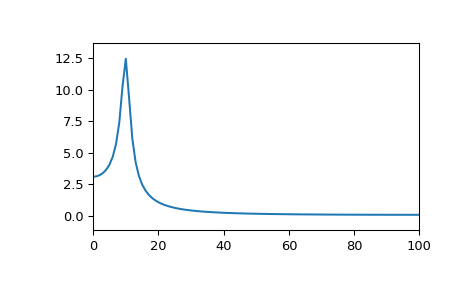
虽然 DFT 总是沿着单位圆对 Z 变换进行采样，但线性调频 Z 变换允许我们沿着任何对数螺旋（例如半径小于 1 的圆）对 Z 变换进行采样

>>> M = fs // 2  # Just positive frequencies, like rfft
>>> a = np.exp(-f1/fs)  # Starting point of the circle, radius < 1
>>> w = np.exp(-1j*np.pi/M)  # "Step size" of circle
>>> points = czt_points(M + 1, w, a)  # M + 1 to include Nyquist
>>> plt.plot(points.real, points.imag, '.')
>>> plt.gca().add_patch(plt.Circle((0,0), radius=1, fill=False, alpha=.3))
>>> plt.axis('equal'); plt.axis([-1.05, 1.05, -0.05, 1.05])
>>> plt.show()

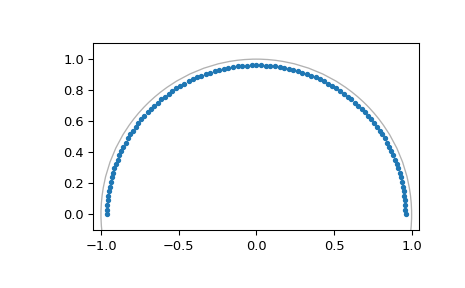
使用正确的半径，这可以在不产生频谱泄漏的情况下变换衰减正弦波（以及具有相同衰减率的其他波形）

>>> z_vals = czt(x, M + 1, w, a)  # Include Nyquist for comparison to rfft
>>> freqs = np.angle(points)*fs/(2*np.pi)  # angle = omega, radius = sigma
>>> plt.plot(freqs, abs(z_vals))
>>> plt.margins(0, 0.1)
>>> plt.show()