scipy.signal.

zoom_fft

scipy.signal.zoom_fft(x, fn, m=None, *, fs=2, endpoint=False, axis=-1)

计算 x 的 DFT，仅针对 fn 范围内的频率。

参数:

x数组

要变换的信号。

fn类数组

一个长度为2的序列 [f1, f2] 表示频率范围，或一个标量，此时假定范围为 [0, fn]。

m整型, 可选

要计算的点数。默认值为 x 的长度。

fs浮点型, 可选

采样频率。例如，如果 fs=10 表示 10 kHz，则 f1 和 f2 也将以 kHz 为单位给出。默认采样频率为 2，因此 f1 和 f2 应在 [0, 1] 范围内，以使变换保持在奈奎斯特频率以下。

endpoint布尔型, 可选

如果为 True，则 f2 是最后一个采样点。否则，它不包含在内。默认为 False。

axis整型, 可选

计算 FFT 的轴。如果未给出，则使用最后一个轴。

返回:

outndarray

变换后的信号。傅里叶变换将在点 f1, f1+df, f1+2df, …, f2 处计算，其中 df=(f2-f1)/m。

另请参阅

ZoomFFT

创建可调用部分 FFT 函数的类。

说明

选择默认值是为了使 signal.zoom_fft(x, 2) 等效于 fft.fft(x)；并且，如果 m > len(x)，则 signal.zoom_fft(x, 2, m) 等效于 fft.fft(x, m)。

要绘制结果变换的幅度图，请使用

plot(linspace(f1, f2, m, endpoint=False), abs(zoom_fft(x, [f1, f2], m)))

如果需要重复变换，请使用 ZoomFFT 来构建一个专门的变换函数，该函数可以重复使用而无需重新计算常量。

示例

在浏览器中试用！

要绘制变换结果图，请使用以下类似代码

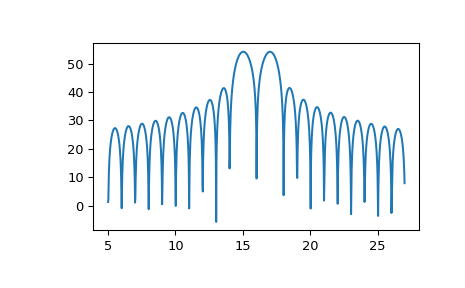
>>> import numpy as np
>>> from scipy.signal import zoom_fft
>>> t = np.linspace(0, 1, 1021)
>>> x = np.cos(2*np.pi*15*t) + np.sin(2*np.pi*17*t)
>>> f1, f2 = 5, 27
>>> X = zoom_fft(x, [f1, f2], len(x), fs=1021)
>>> f = np.linspace(f1, f2, len(x))
>>> import matplotlib.pyplot as plt
>>> plt.plot(f, 20*np.log10(np.abs(X)))
>>> plt.show()

返回在新标签页中打开