scipy.signal.

CZT#

class scipy.signal.CZT(n, m=None, w=None, a=1 + 0j)[源码]#

创建一个可调用的Chirp Z变换函数。

用于计算围绕螺旋线频率响应的变换。此类的对象是可调用对象，可以对其输入执行Chirp Z变换。此对象会预先计算给定变换中使用的常数Chirp。

参数:

nint: 信号的大小。
mint, 可选: 所需的输出点数。默认值为 n。
wcomplex, 可选: 每步点之间的比率。这必须精确，否则累积误差会降低输出序列的尾部质量。默认为单位圆周围等间距的点。
acomplex, 可选: 复平面中的起始点。默认值为 1+0j。

方法

`__call__`(x, *[, axis])	计算信号的Chirp Z变换。
`点`()	返回计算Chirp Z变换的点。

返回:

fCZT: 用于计算x上Chirp Z变换的可调用对象f(x, axis=-1)。

另请参阅

czt: 用于快速计算CZT的便捷函数。
ZoomFFT: 创建可调用部分FFT函数的类。

注意

默认设置使得f(x)等同于fft.fft(x)，并且如果m > len(x)，则f(x, m)等同于fft.fft(x, m)。

如果w不在单位圆上，则变换将围绕半径呈指数增长的螺旋线进行。无论如何，角度将线性增加。

对于位于单位圆上的变换，使用ZoomFFT时精度更佳，因为w中的任何数值误差会在长数据长度下累积，从而偏离单位圆。

Chirp Z变换可能比等效的零填充FFT更快。你可以用你自己的数组大小来试试看。

然而，Chirp Z变换的精度远低于等效的零填充FFT。

由于此CZT是使用Bluestein算法实现的，因此它可以在O(N log N)时间内计算大素数长度的傅里叶变换，而不是直接DFT计算所需的O(N**2)时间。（scipy.fft也使用Bluestein算法。）

（“Chirp Z变换”这个名称来源于Bluestein算法中Chirp信号的使用。它不像其他名称中带有“Chirp”的变换那样将信号分解为Chirp信号。）

参考文献

[1]

Leo I. Bluestein, “A linear filtering approach to the computation of the discrete Fourier transform,” Northeast Electronics Research and Engineering Meeting Record 10, 218-219 (1968).

[2]

Rabiner, Schafer, and Rader, “The chirp z-transform algorithm and its application,” Bell Syst. Tech. J. 48, 1249-1292 (1969).

示例

计算多个素数长度的FFT

>>> from scipy.signal import CZT
>>> import numpy as np
>>> a = np.random.rand(7)
>>> b = np.random.rand(7)
>>> c = np.random.rand(7)
>>> czt_7 = CZT(n=7)
>>> A = czt_7(a)
>>> B = czt_7(b)
>>> C = czt_7(c)

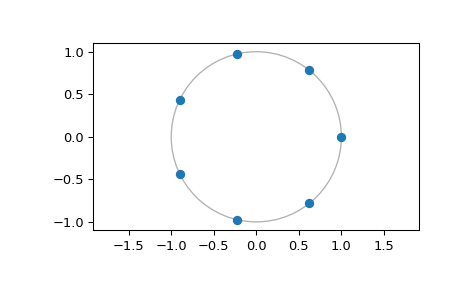
显示计算FFT的点

>>> czt_7.points()
array([ 1.00000000+0.j        ,  0.62348980+0.78183148j,
       -0.22252093+0.97492791j, -0.90096887+0.43388374j,
       -0.90096887-0.43388374j, -0.22252093-0.97492791j,
        0.62348980-0.78183148j])
>>> import matplotlib.pyplot as plt
>>> plt.plot(czt_7.points().real, czt_7.points().imag, 'o')
>>> plt.gca().add_patch(plt.Circle((0,0), radius=1, fill=False, alpha=.3))
>>> plt.axis('equal')
>>> plt.show()