scipy.stats.wishart#

scipy.stats.wishart = <scipy.stats._multivariate.wishart_gen object>[源代码]#

Wishart 随机变量。

df 关键字指定自由度。scale 关键字指定比例矩阵，该矩阵必须是对称且正定的。在这种上下文中，比例矩阵通常根据多元正态精度矩阵（协方差矩阵的逆矩阵）来解释。这些参数必须满足关系式 df > scale.ndim - 1，但请参阅关于将 rvs 方法与 df < scale.ndim 一起使用的说明。

参数:

dfint: 自由度，必须大于或等于比例矩阵的维度
scalearray_like: 分布的对称正定比例矩阵
seed{None, int, np.random.RandomState, np.random.Generator}, optional: 用于绘制随机变量。如果 seed 为 None，则使用 RandomState 单例。如果 seed 是一个整数，则使用一个新的 RandomState 实例，并使用 seed 作为种子。如果 seed 已经是一个 RandomState 或 Generator 实例，则使用该对象。默认为 None。

方法

pdf(x, df, scale)	概率密度函数。
logpdf(x, df, scale)	概率密度函数的对数。
rvs(df, scale, size=1, random_state=None)	从 Wishart 分布中抽取随机样本。
entropy()	计算 Wishart 分布的微分熵。

引发:

scipy.linalg.LinAlgError: 如果比例矩阵 scale 不是正定的。

参见

invwishart, chi2

注释

比例矩阵 scale 必须是对称正定矩阵。不支持奇异矩阵，包括对称正半定情况。不检查对称性；仅使用下三角部分。

Wishart 分布通常表示为

\[W_p(\nu, \Sigma)\]

其中 \(\nu\) 是自由度，\(\Sigma\) 是 \(p \times p\) 比例矩阵。

wishart 的概率密度函数支持正定矩阵 \(S\)；如果 \(S \sim W_p(\nu, \Sigma)\)，则其 PDF 由下式给出

\[f(S) = \frac{|S|^{\frac{\nu - p - 1}{2}}}{2^{ \frac{\nu p}{2} } |\Sigma|^\frac{\nu}{2} \Gamma_p \left ( \frac{\nu}{2} \right )} \exp\left( -tr(\Sigma^{-1} S) / 2 \right)\]

如果 \(S \sim W_p(\nu, \Sigma)\) (Wishart)，则 \(S^{-1} \sim W_p^{-1}(\nu, \Sigma^{-1})\) (逆 Wishart)。

如果比例矩阵是一维且等于 1，则 Wishart 分布 \(W_1(\nu, 1)\) 坍缩为 \(\chi^2(\nu)\) 分布。

由 rvs 方法实现的算法 [2] 可能会产生具有 \(p - 1 < \nu < p\) 的数值奇异矩阵；用户可能希望检查此条件并在必要时生成替换样本。

版本 0.16.0 中新增。

参考

[1]

M.L. Eaton, “Multivariate Statistics: A Vector Space Approach”, Wiley, 1983.

[2]

W.B. Smith and R.R. Hocking, “Algorithm AS 53: Wishart Variate Generator”, Applied Statistics, vol. 21, pp. 341-345, 1972.

示例

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import wishart, chi2
>>> x = np.linspace(1e-5, 8, 100)
>>> w = wishart.pdf(x, df=3, scale=1); w[:5]
array([ 0.00126156,  0.10892176,  0.14793434,  0.17400548,  0.1929669 ])
>>> c = chi2.pdf(x, 3); c[:5]
array([ 0.00126156,  0.10892176,  0.14793434,  0.17400548,  0.1929669 ])
>>> plt.plot(x, w)
>>> plt.show()

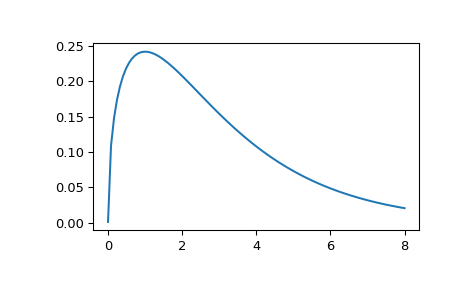
../../_images/scipy-stats-wishart-1_00_00.png

输入分位数可以是任何形状的数组，只要最后一个轴标记了组件。

或者，可以调用该对象（作为一个函数）来固定自由度和比例参数，从而返回“冻结”的 Wishart 随机变量

>>> rv = wishart(df=1, scale=1)
>>> # Frozen object with the same methods but holding the given
>>> # degrees of freedom and scale fixed.