tukey_hsd#
- scipy.stats.tukey_hsd(*args, equal_var=True)[source]#
对多个处理的均值相等性执行 Tukey 的 HSD 检验。
Tukey 的诚实显著差异 (HSD) 检验对一组样本的均值进行成对比较。 尽管 ANOVA(例如
f_oneway)评估每个样本的基础真实均值是否相同,但 Tukey 的 HSD 是一种事后检验,用于将每个样本的均值与其他每个样本的均值进行比较。零假设是样本的基础分布都具有相同的均值。 对于每种可能的样本配对,都会计算检验统计量,该统计量只是样本均值之间的差异。 对于每一对,p 值是零假设(和其他假设;参见注释)下观察到如此极端的统计量值的概率,考虑到正在执行许多成对比较。 还可以获得每对均值之间差异的置信区间。
- 参数:
- 返回:
- result
TukeyHSDResult实例 返回值是一个具有以下属性的对象
- statisticfloat ndarray
每个比较的计算出的检验统计量。 索引
(i, j)处的元素是组i和j之间比较的统计量。- pvaluefloat ndarray
每个比较的计算出的 p 值。 索引
(i, j)处的元素是组i和j之间比较的 p 值。
该对象具有以下方法
- confidence_interval(confidence_level=0.95)
计算指定置信水平的置信区间。
- result
参见
dunnett执行均值与对照组的比较。
注释
此检验的使用依赖于几个假设。
观察结果在组内和组间是独立的。
每个组内的观察结果呈正态分布。
绘制样本的分布具有相同的有限方差。
该检验的原始公式是针对从假定具有相等方差的总体中抽取的相等大小的样本 [6]。 如果样本大小不相等,则检验使用 Tukey-Kramer 方法 [4]。 当不假定方差相等(
equal_var=False)时,检验使用 Games-Howell 方法 [7]。参考文献
[1]NIST/SEMATECH 电子统计方法手册,“7.4.7.1. Tukey 的方法。” https://www.itl.nist.gov/div898/handbook/prc/section4/prc471.htm, 2020 年 11 月 28 日。
[2]Abdi, Herve & Williams, Lynne. (2021). “Tukey's Honestly Significant Difference (HSD) Test.” https://personal.utdallas.edu/~herve/abdi-HSD2010-pretty.pdf
[3]“One-Way ANOVA Using SAS PROC ANOVA & PROC GLM.” SAS Tutorials, 2007, www.stattutorials.com/SAS/TUTORIAL-PROC-GLM.htm.
[4] (1,2)Kramer, Clyde Young. “Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications.” Biometrics, vol. 12, no. 3, 1956, pp. 307-310. JSTOR, www.jstor.org/stable/3001469. Accessed 25 May 2021.
[5]NIST/SEMATECH 电子统计方法手册,“7.4.3.3. ANOVA 表和关于均值的假设检验” https://www.itl.nist.gov/div898/handbook/prc/section4/prc433.htm, 2021 年 6 月 2 日。
[6]Tukey, John W. “Comparing Individual Means in the Analysis of Variance.” Biometrics, vol. 5, no. 2, 1949, pp. 99-114. JSTOR, www.jstor.org/stable/3001913. Accessed 14 June 2021.
[7] (1,2)P. A. Games and J. F. Howell, “Pairwise Multiple Comparison Procedures with Unequal N’s and/or Variances: A Monte Carlo Study,” Journal of Educational Statistics, vol. 1, no. 2, pp. 113-125, Jun. 1976, doi: https://doi.org/10.3102/10769986001002113.
示例
以下是一些比较三种品牌头痛药缓解时间的数据,以分钟为单位报告。 数据改编自 [3]。
>>> import numpy as np >>> from scipy.stats import tukey_hsd >>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9] >>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1] >>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]
我们想看看任何组之间的均值是否显着不同。 首先,直观地检查箱须图。
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1) >>> ax.boxplot([group0, group1, group2]) >>> ax.set_xticklabels(["group0", "group1", "group2"]) >>> ax.set_ylabel("mean") >>> plt.show()
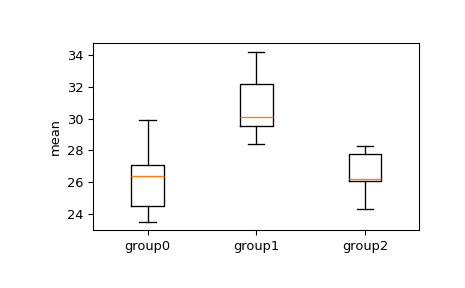
从箱须图中,我们可以看到第 1 组到第 2 组和第 3 组的四分位间距重叠,但我们可以应用
tukey_hsd检验来确定均值之间的差异是否显着。 我们设置了 .05 的显着性水平来拒绝零假设。>>> res = tukey_hsd(group0, group1, group2) >>> print(res) Pairwise Group Comparisons (95.0% Confidence Interval) Comparison Statistic p-value Lower CI Upper CI (0 - 1) -4.600 0.014 -8.249 -0.951 (0 - 2) -0.260 0.980 -3.909 3.389 (1 - 0) 4.600 0.014 0.951 8.249 (1 - 2) 4.340 0.020 0.691 7.989 (2 - 0) 0.260 0.980 -3.389 3.909 (2 - 1) -4.340 0.020 -7.989 -0.691
零假设是每个组都具有相同的均值。
group0和group1以及group1和group2之间比较的 p 值不超过 .05,因此我们拒绝它们具有相同均值的零假设。group0和group2之间比较的 p 值超过 .05,因此我们接受零假设,即它们的均值之间没有显着差异。我们还可以计算与我们选择的置信水平相关的置信区间。
>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9] >>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1] >>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8] >>> result = tukey_hsd(group0, group1, group2) >>> conf = res.confidence_interval(confidence_level=.99) >>> for ((i, j), l) in np.ndenumerate(conf.low): ... # filter out self comparisons ... if i != j: ... h = conf.high[i,j] ... print(f"({i} - {j}) {l:>6.3f} {h:>6.3f}") (0 - 1) -9.480 0.280 (0 - 2) -5.140 4.620 (1 - 0) -0.280 9.480 (1 - 2) -0.540 9.220 (2 - 0) -4.620 5.140 (2 - 1) -9.220 0.540