scipy.stats.

siegelslopes#

scipy.stats.siegelslopes(y, x=None, method='hierarchical', *, axis=None, nan_policy='propagate', keepdims=False)[源代码]#

计算一组点 (x, y) 的 Siegel 估计量。

siegelslopes 实现了一种使用重复中位数进行稳健线性回归的方法（参见 [1]）以将直线拟合到点 (x, y)。该方法对异常值具有鲁棒性，具有 50% 的渐近击穿点。

参数:
yarray_like

因变量。

xarray_like 或 None, 可选

自变量。如果为 None，则使用 arange(len(y)) 代替。

method{‘hierarchical’, ‘separate’}

如果为 ‘hierarchical’，则使用估计斜率 slope 估计截距（默认选项）。如果为 ‘separate’，则独立于估计斜率估计截距。有关详细信息，请参见 Notes。

axisint 或 None, 默认值: None

如果为 int，则为计算统计量所沿的输入轴。输入的每个轴切片（例如，行）的统计量将出现在输出的相应元素中。如果为 None，则在计算统计量之前将展平输入。

nan_policy{‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入 NaN。

  • propagate: 如果在计算统计量的轴切片（例如，行）中存在 NaN，则输出的相应条目将为 NaN。

  • omit: 执行计算时将省略 NaN。如果在计算统计量的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。

  • raise: 如果存在 NaN，将引发 ValueError。

keepdimsbool, 默认值: False

如果将其设置为 True，则减小的轴将作为大小为 1 的维度保留在结果中。使用此选项，结果将正确地广播到输入数组。

返回值:
resultSiegelslopesResult 实例

返回值是一个具有以下属性的对象

slopefloat

回归线的斜率估计。

interceptfloat

回归线的截距估计。

参见

theilslopes

一种没有重复中位数的类似技术

注释

使用 n = len(y)，将 m_j 计算为从点 (x[j], y[j]) 到所有其他 n-1 个点的斜率的中位数。slope 然后是所有斜率 m_j 的中位数。在 [1] 中给出了两种估计截距的方法，可以通过参数 method 进行选择。分层方法使用估计的斜率 slope 并将 intercept 计算为 y - slope*x 的中位数。另一种方法分别估计截距，如下所示：对于每个点 (x[j], y[j])，计算通过剩余点的所有 n-1 条线的截距，并取中位数 i_j。intercept 是 i_j 的中位数。

该实现计算 n 次大小为 n 的向量的中位数，对于大型向量来说，这可能会很慢。有一些更有效的算法（参见 [2]），但此处未实现。

为了与旧版本的 SciPy 兼容，返回值的作用类似于长度为 2 的 namedtuple，字段为 slope 和 intercept，因此可以继续编写

slope, intercept = siegelslopes(y, x)

从 SciPy 1.9 开始，np.matrix 输入（不建议用于新代码）在执行计算之前会转换为 np.ndarray。在这种情况下，输出将是标量或具有适当形状的 np.ndarray，而不是 2D np.matrix。同样，虽然会忽略屏蔽数组的屏蔽元素，但输出将是标量或 np.ndarray，而不是 mask=False 的屏蔽数组。

参考文献

[1] (1,2)

A. Siegel, “Robust Regression Using Repeated Medians”, Biometrika, Vol. 69, pp. 242-244, 1982.

[2]

A. Stein and M. Werman, “Finding the repeated median regression line”, Proceedings of the Third Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 409-413, 1992.

示例

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-5, 5, num=150)
>>> y = x + np.random.normal(size=x.size)
>>> y[11:15] += 10  # add outliers
>>> y[-5:] -= 7

计算斜率和截距。为了进行比较，还使用 linregress 计算最小二乘拟合

>>> res = stats.siegelslopes(y, x)
>>> lsq_res = stats.linregress(x, y)

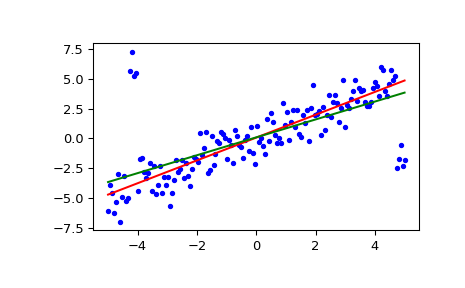
绘制结果。Siegel 回归线以红色显示。绿线显示用于比较的最小二乘拟合。

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, y, 'b.')
>>> ax.plot(x, res[1] + res[0] * x, 'r-')
>>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-')
>>> plt.show()
../../_images/scipy-stats-siegelslopes-1.png
在此页面上