scipy.stats.
ppcc_max#
- scipy.stats.ppcc_max(x, brack=(0.0, 1.0), dist='tukeylambda')[source]#
计算最大化 PPCC 的形状参数。
概率图相关系数 (PPCC) 图可用于确定单参数分布族的最优形状参数。
ppcc_max返回形状参数,该参数将使给定数据到单参数分布族的概率图相关系数最大化。- 参数:
- xarray_like
输入数组。
- bracktuple, optional
三元组 (a,b,c) 其中 (a<b<c)。如果 bracket 由两个数字 (a, c) 组成,则它们被假定为下坡 bracket 搜索的起始区间(参见
scipy.optimize.brent)。- diststr 或 stats.distributions 实例, optional
分布或分布函数名称。 看起来很像 stats.distributions 实例的对象(即它们有一个
ppf方法)也被接受。 默认为'tukeylambda'。
- 返回:
- shape_valuefloat
概率图相关系数达到其最大值的形状参数。
注释
brack 关键字用作起始点,这在极端情况下很有用。 可以使用绘图来获得最大值位置的粗略视觉估计,以便在其附近开始搜索。
参考文献
[1]J.J. Filliben, “The Probability Plot Correlation Coefficient Test for Normality”, Technometrics, Vol. 17, pp. 111-117, 1975.
[2]Engineering Statistics Handbook, NIST/SEMATEC, https://www.itl.nist.gov/div898/handbook/eda/section3/ppccplot.htm
示例
首先,我们从形状参数为 2.5 的 Weibull 分布中生成一些随机数据
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> c = 2.5 >>> x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)
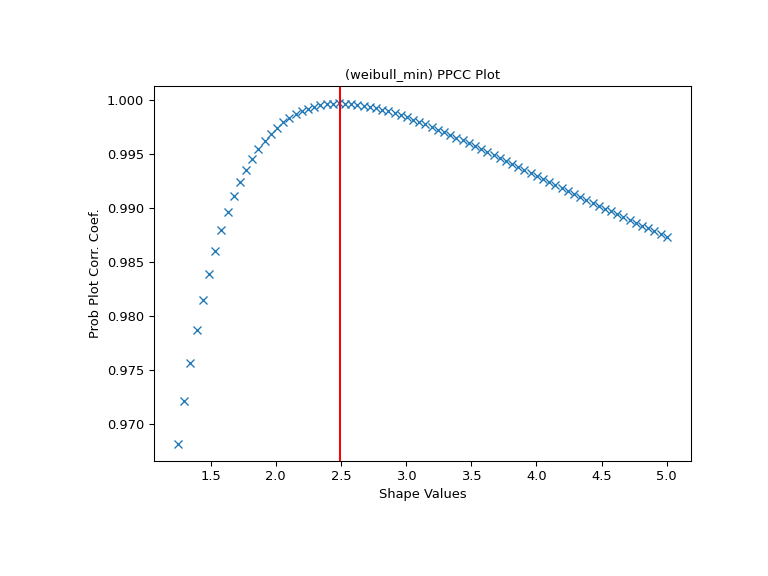
使用 Weibull 分布为此数据生成 PPCC 图。
>>> fig, ax = plt.subplots(figsize=(8, 6)) >>> res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax)
我们计算形状应该达到其最大值的位置,并在那里绘制一条红线。 该线应与 PPCC 图中的最高点重合。
>>> cmax = stats.ppcc_max(x, brack=(c/2, 2*c), dist='weibull_min') >>> ax.axvline(cmax, color='r') >>> plt.show()