scipy.stats.

ppcc_plot

scipy.stats.ppcc_plot(x, a, b, dist='tukeylambda', plot=None, N=80)

计算并可选地绘制概率图相关系数。

概率图相关系数 (PPCC) 图可用于确定单参数分布族的最优形状参数。它不能用于没有形状参数（如正态分布）或具有多个形状参数的分布。

默认情况下，使用 Tukey-Lambda 分布 (stats.tukeylambda)。 Tukey-Lambda PPCC 图通过近似正态分布从长尾分布插值到短尾分布，因此在实践中特别有用。

参数:

xarray_like

输入数组。

a, b标量

要使用的形状参数的下限和上限。

diststr 或 stats.distributions 实例，可选

分布或分布函数名称。也接受看起来足够像 stats.distributions 实例的对象（即，它们具有 ppf 方法）。默认值为 'tukeylambda'。

plotobject，可选

如果给定，则绘制 PPCC 与形状参数的关系。plot 是一个必须具有方法“plot”和“text”的对象。可以使用matplotlib.pyplot 模块或 Matplotlib Axes 对象，或者具有相同方法的自定义对象。默认值为 None，这意味着不创建绘图。

Nint，可选

水平轴上的点数（从 a 到 b 均匀分布）。

返回:

svalsndarray

计算 ppcc 的形状值。

ppccndarray

计算出的概率图相关系数值。

参见

ppcc_max, probplot, boxcox_normplot, tukeylambda

参考文献

J.J. Filliben, “The Probability Plot Correlation Coefficient Test for Normality”, Technometrics, Vol. 17, pp. 111-117, 1975.

示例

在您的浏览器中尝试一下！

首先，我们从形状参数为 2.5 的 Weibull 分布生成一些随机数据，并绘制数据的直方图

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> c = 2.5
>>> x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)

看看数据的直方图。

>>> fig1, ax = plt.subplots(figsize=(9, 4))
>>> ax.hist(x, bins=50)
>>> ax.set_title('Histogram of x')
>>> plt.show()

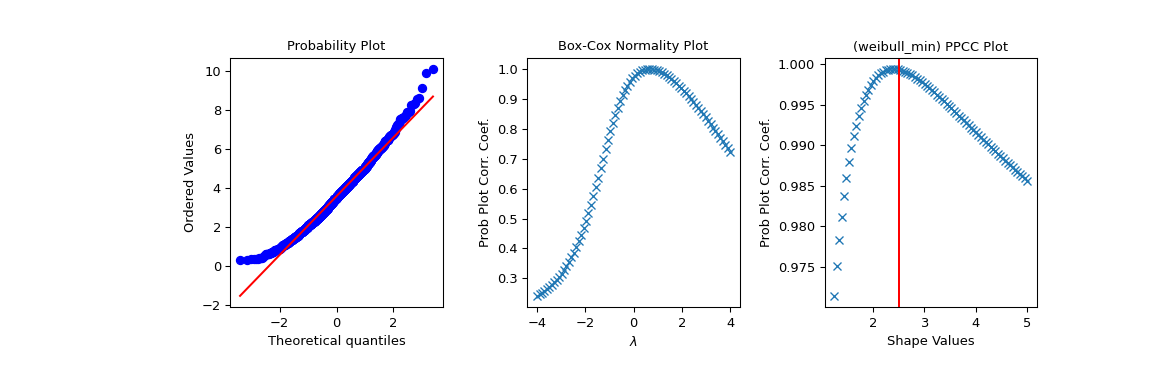
现在，我们使用 PPCC 图以及相关的概率图和 Box-Cox 正态图来探索此数据。 在我们期望 PPCC 值最大（在上面使用的形状参数 c 处）的地方绘制一条红线

>>> fig2 = plt.figure(figsize=(12, 4))
>>> ax1 = fig2.add_subplot(1, 3, 1)
>>> ax2 = fig2.add_subplot(1, 3, 2)
>>> ax3 = fig2.add_subplot(1, 3, 3)
>>> res = stats.probplot(x, plot=ax1)
>>> res = stats.boxcox_normplot(x, -4, 4, plot=ax2)
>>> res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax3)
>>> ax3.axvline(c, color='r')
>>> plt.show()

返回在新标签页中打开