scipy.stats.

gzscore#

scipy.stats.gzscore(a, *, axis=0, ddof=0, nan_policy='propagate')[source]#

计算几何标准分。

计算样本中每个严格正值的几何 z 分数，相对于几何平均值和标准差。 从数学上讲，几何 z 分数可以评估为

gzscore = log(a/gmu) / log(gsigma)

其中 gmu（或 gsigma）是几何平均值（或标准差）。

参数:
aarray_like

样本数据。

axisint 或 None，可选

要沿其操作的轴。 默认为 0。如果为 None，则计算整个数组 a。

ddofint，可选

标准差计算中的自由度校正。 默认为 0。

nan_policy{‘propagate’, ‘raise’, ‘omit’}, 可选

定义如何处理输入包含 nan 时的情况。 “propagate”返回 nan，“raise”引发错误，“omit”执行计算时忽略 nan 值。 默认为“propagate”。 请注意，当值为“omit”时，输入中的 nan 也会传播到输出，但它们不会影响为非 nan 值计算的几何 z 分数。

返回:
gzscorearray_like

几何 z 分数，通过输入数组 a 的几何平均值和几何标准差标准化。

另请参见

gmean

几何平均值

gstd

几何标准差

zscore

标准分

注释

此函数保留 ndarray 子类，并且还可用于矩阵和屏蔽数组（它对参数使用 asanyarray 而不是 asarray）。

在 1.8 版本中添加。

gzscore 除了 NumPy 之外，还对 Python Array API Standard 兼容后端具有实验性支持。 请考虑通过设置环境变量 SCIPY_ARRAY_API=1 并提供 CuPy、PyTorch、JAX 或 Dask 数组作为数组参数来测试这些功能。 支持以下后端和设备（或其他功能）的组合。

库

CPU

GPU

NumPy

✅

不适用

CuPy

不适用

✅

PyTorch

✅

✅

JAX

✅

✅

Dask

✅

不适用

有关更多信息，请参见 对数组 API 标准的支持。

参考

示例

从对数正态分布中抽取样本

>>> import numpy as np
>>> from scipy.stats import zscore, gzscore
>>> import matplotlib.pyplot as plt

>>> rng = np.random.default_rng()
>>> mu, sigma = 3., 1.  # mean and standard deviation
>>> x = rng.lognormal(mu, sigma, size=500)

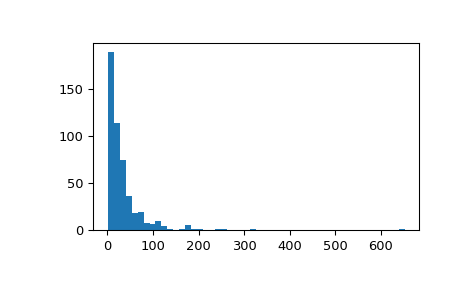
显示样本的直方图

>>> fig, ax = plt.subplots()
>>> ax.hist(x, 50)
>>> plt.show()
../../_images/scipy-stats-gzscore-1_00_00.png

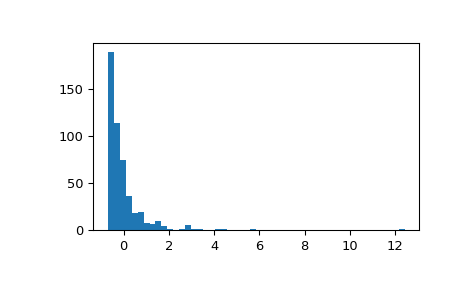
显示由经典 zscore 标准化的样本的直方图。 分布已重新缩放，但其形状未改变。

>>> fig, ax = plt.subplots()
>>> ax.hist(zscore(x), 50)
>>> plt.show()
../../_images/scipy-stats-gzscore-1_01_00.png

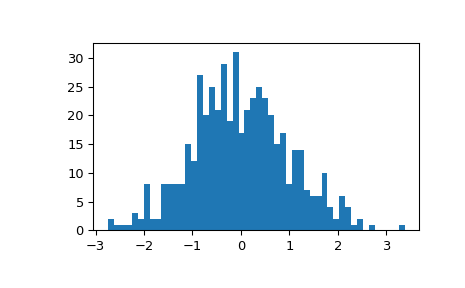
证明几何 zscore 的分布已重新缩放并接近正态分布

>>> fig, ax = plt.subplots()
>>> ax.hist(gzscore(x), 50)
>>> plt.show()
../../_images/scipy-stats-gzscore-1_02_00.png
在本页上