scipy.special.tklmbda#
- scipy.special.tklmbda(x, lmbda, out=None) = <ufunc 'tklmbda'>#
Tukey lambda 分布的累积分布函数。
- 参数:
- x, lmbdaarray_like
参数
- outndarray, optional
函数结果的可选输出数组
- 返回:
- cdf标量或 ndarray
Tukey lambda CDF 的值
另请参阅
scipy.stats.tukeylambdaTukey lambda 分布
示例
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.special import tklmbda, expit
计算 Tukey lambda 分布在
lmbda= -1.5 时的多个x值的累积分布函数 (CDF)。>>> x = np.linspace(-2, 2, 9) >>> x array([-2. , -1.5, -1. , -0.5, 0. , 0.5, 1. , 1.5, 2. ]) >>> tklmbda(x, -1.5) array([0.34688734, 0.3786554 , 0.41528805, 0.45629737, 0.5 , 0.54370263, 0.58471195, 0.6213446 , 0.65311266])
当
lmbda为 0 时,该函数是逻辑 S 形函数,在scipy.special中以expit实现。>>> tklmbda(x, 0) array([0.11920292, 0.18242552, 0.26894142, 0.37754067, 0.5 , 0.62245933, 0.73105858, 0.81757448, 0.88079708]) >>> expit(x) array([0.11920292, 0.18242552, 0.26894142, 0.37754067, 0.5 , 0.62245933, 0.73105858, 0.81757448, 0.88079708])
当
lmbda为 1 时,Tukey lambda 分布在区间 [-1, 1] 上是均匀的,因此 CDF 线性增加。>>> t = np.linspace(-1, 1, 9) >>> tklmbda(t, 1) array([0. , 0.125, 0.25 , 0.375, 0.5 , 0.625, 0.75 , 0.875, 1. ])
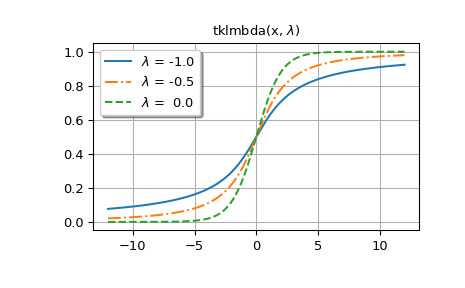
在下文中,我们将生成
lmbda几个值的图。第一张图显示了
lmbda<= 0 的图。>>> styles = ['-', '-.', '--', ':'] >>> fig, ax = plt.subplots() >>> x = np.linspace(-12, 12, 500) >>> for k, lmbda in enumerate([-1.0, -0.5, 0.0]): ... y = tklmbda(x, lmbda) ... ax.plot(x, y, styles[k], label=rf'$\lambda$ = {lmbda:-4.1f}')
>>> ax.set_title(r'tklmbda(x, $\lambda$)') >>> ax.set_label('x') >>> ax.legend(framealpha=1, shadow=True) >>> ax.grid(True)
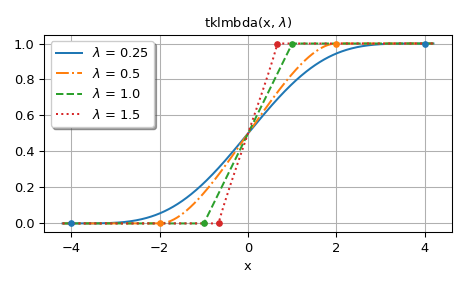
第二张图显示了
lmbda> 0 的图。图中的点表示分布支持的边界。>>> fig, ax = plt.subplots() >>> x = np.linspace(-4.2, 4.2, 500) >>> lmbdas = [0.25, 0.5, 1.0, 1.5] >>> for k, lmbda in enumerate(lmbdas): ... y = tklmbda(x, lmbda) ... ax.plot(x, y, styles[k], label=fr'$\lambda$ = {lmbda}')
>>> ax.set_prop_cycle(None) >>> for lmbda in lmbdas: ... ax.plot([-1/lmbda, 1/lmbda], [0, 1], '.', ms=8)
>>> ax.set_title(r'tklmbda(x, $\lambda$)') >>> ax.set_xlabel('x') >>> ax.legend(framealpha=1, shadow=True) >>> ax.grid(True)
>>> plt.tight_layout() >>> plt.show()
Tukey lambda 分布的 CDF 也作为
scipy.stats.tukeylambda的cdf方法实现。在下文中,tukeylambda.cdf(x, -0.5)和tklmbda(x, -0.5)计算相同的值>>> from scipy.stats import tukeylambda >>> x = np.linspace(-2, 2, 9)
>>> tukeylambda.cdf(x, -0.5) array([0.21995157, 0.27093858, 0.33541677, 0.41328161, 0.5 , 0.58671839, 0.66458323, 0.72906142, 0.78004843])
>>> tklmbda(x, -0.5) array([0.21995157, 0.27093858, 0.33541677, 0.41328161, 0.5 , 0.58671839, 0.66458323, 0.72906142, 0.78004843])
tukeylambda中的实现还提供了位置和比例参数,以及其他方法,例如pdf()(概率密度函数) 和ppf()(CDF 的逆),因此对于处理 Tukey lambda 分布,tukeylambda更具通用性。tklmbda的主要优点是它比tukeylambda.cdf快得多。