scipy.special.shichi#
- scipy.special.shichi(x, out=None) = <ufunc 'shichi'>#
双曲正弦和余弦积分。
双曲正弦积分是
\[\int_0^x \frac{\sinh{t}}{t}dt\]双曲余弦积分是
\[\gamma + \log(x) + \int_0^x \frac{\cosh{t} - 1}{t} dt\]其中 \(\gamma\) 是欧拉常数,\(\log\) 是对数的principal branch [1]。
- 参数:
- xarray_like
计算双曲正弦和余弦积分的实数或复数点。
- outtuple of ndarray, optional
用于函数结果的可选输出数组
- 返回值:
- si标量或 ndarray
在
x处的双曲正弦积分- ci标量或 ndarray
在
x处的双曲余弦积分
注释
对于
x < 0的实数参数,chi是双曲余弦积分的实部。对于这些点,chi(x)和chi(x + 0j)相差一个因子1j*pi。对于实数参数,该函数通过调用 Cephes 的 [2] shichi 例程来计算。对于复数参数,该算法基于 Mpmath 的 [3] shi 和 chi 例程。
参考文献
[1]Milton Abramowitz 和 Irene A. Stegun,编辑。《数学函数手册,包含公式、图表和数学表》。纽约:Dover,1972。(参见第 5.2 节。)
[2]Cephes 数学函数库,http://www.netlib.org/cephes/
[3]Fredrik Johansson 和其他人。“mpmath:用于任意精度浮点运算的 Python 库”(版本 0.19)http://mpmath.org/
示例
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.special import shichi, sici
shichi接受实数或复数输入>>> shichi(0.5) (0.5069967498196671, -0.05277684495649357) >>> shichi(0.5 + 2.5j) ((0.11772029666668238+1.831091777729851j), (0.29912435887648825+1.7395351121166562j))
双曲正弦和余弦积分 Shi(z) 和 Chi(z) 与正弦和余弦积分 Si(z) 和 Ci(z) 的关系为
Shi(z) = -i*Si(i*z)
Chi(z) = Ci(-i*z) + i*pi/2
>>> z = 0.25 + 5j >>> shi, chi = shichi(z) >>> shi, -1j*sici(1j*z)[0] # Should be the same. ((-0.04834719325101729+1.5469354086921228j), (-0.04834719325101729+1.5469354086921228j)) >>> chi, sici(-1j*z)[1] + 1j*np.pi/2 # Should be the same. ((-0.19568708973868087+1.556276312103824j), (-0.19568708973868087+1.556276312103824j))
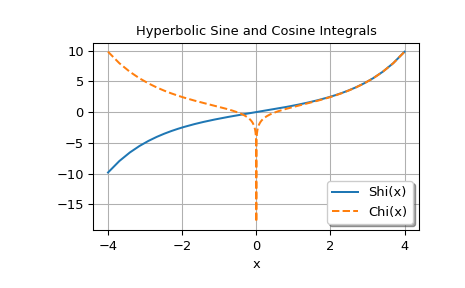
绘制在实轴上评估的函数
>>> xp = np.geomspace(1e-8, 4.0, 250) >>> x = np.concatenate((-xp[::-1], xp)) >>> shi, chi = shichi(x)
>>> fig, ax = plt.subplots() >>> ax.plot(x, shi, label='Shi(x)') >>> ax.plot(x, chi, '--', label='Chi(x)') >>> ax.set_xlabel('x') >>> ax.set_title('Hyperbolic Sine and Cosine Integrals') >>> ax.legend(shadow=True, framealpha=1, loc='lower right') >>> ax.grid(True) >>> plt.show()