scipy.special.kolmogorov#

scipy.special.kolmogorov(y, out=None) = <ufunc 'kolmogorov'>#

柯尔莫哥洛夫分布的互补累积分布（生存函数）函数。

返回柯尔莫哥洛夫的极限分布互补累积分布函数（随着 n 趋于无穷大，D_n*\sqrt(n)）在经验分布和理论分布之间进行相等性的双边检验。它等于（n 趋于无穷大的极限）具有以下概率，sqrt(n) * max absolute deviation > y。

参数:
y浮点数 array_like

经验 CDF (ECDF) 和目标 CDF 之间的绝对偏差，乘以 sqrt(n)。

outndarray，可选

函数结果可选输出数组

返回:
标量或 ndarray

kolmogorov(y) 的值

请参见

kolmogi

该分布的反生存函数

scipy.stats.kstwobign

提供连续分布的功能

smirnov, smirnovi

单边分布函数

备注

kolmogorov 由 stats.kstest 在 Kolmogorov-Smirnov 拟合优度检验中使用。出于历史原因，此函数在 scpy.special 中公开，但实现最准确的 CDF/SF/PDF/PPF/ISF 计算的推荐方法是使用 stats.kstwobign 分布。

范例

显示至少与 0、0.5 和 1.0 一样大的间隙的概率。

>>> import numpy as np
>>> from scipy.special import kolmogorov
>>> from scipy.stats import kstwobign
>>> kolmogorov([0, 0.5, 1.0])
array([ 1.        ,  0.96394524,  0.26999967])

将从拉普拉斯（0, 1）分布获取的 1000 个样本大小的样本与目标分布（法线（0, 1）分布）进行比较。

>>> from scipy.stats import norm, laplace
>>> rng = np.random.default_rng()
>>> n = 1000
>>> lap01 = laplace(0, 1)
>>> x = np.sort(lap01.rvs(n, random_state=rng))
>>> np.mean(x), np.std(x)
(-0.05841730131499543, 1.3968109101997568)

构建经验 CDF 和 K-S 统计量 Dn。

>>> target = norm(0,1)  # Normal mean 0, stddev 1
>>> cdfs = target.cdf(x)
>>> ecdfs = np.arange(n+1, dtype=float)/n
>>> gaps = np.column_stack([cdfs - ecdfs[:n], ecdfs[1:] - cdfs])
>>> Dn = np.max(gaps)
>>> Kn = np.sqrt(n) * Dn
>>> print('Dn=%f, sqrt(n)*Dn=%f' % (Dn, Kn))
Dn=0.043363, sqrt(n)*Dn=1.371265
>>> print(chr(10).join(['For a sample of size n drawn from a N(0, 1) distribution:',
...   ' the approximate Kolmogorov probability that sqrt(n)*Dn>=%f is %f' %
...    (Kn, kolmogorov(Kn)),
...   ' the approximate Kolmogorov probability that sqrt(n)*Dn<=%f is %f' %
...    (Kn, kstwobign.cdf(Kn))]))
For a sample of size n drawn from a N(0, 1) distribution:
 the approximate Kolmogorov probability that sqrt(n)*Dn>=1.371265 is 0.046533
 the approximate Kolmogorov probability that sqrt(n)*Dn<=1.371265 is 0.953467

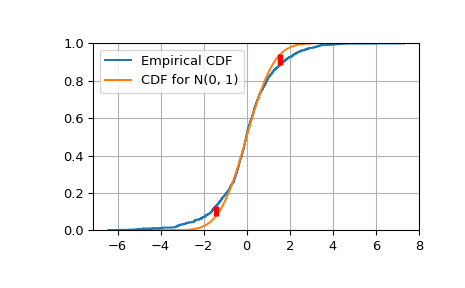
将经验 CDF 与目标 N(0, 1) CDF 作对比。

>>> import matplotlib.pyplot as plt
>>> plt.step(np.concatenate([[-3], x]), ecdfs, where='post', label='Empirical CDF')
>>> x3 = np.linspace(-3, 3, 100)
>>> plt.plot(x3, target.cdf(x3), label='CDF for N(0, 1)')
>>> plt.ylim([0, 1]); plt.grid(True); plt.legend();
>>> # Add vertical lines marking Dn+ and Dn-
>>> iminus, iplus = np.argmax(gaps, axis=0)
>>> plt.vlines([x[iminus]], ecdfs[iminus], cdfs[iminus],
...            color='r', linestyle='dashed', lw=4)
>>> plt.vlines([x[iplus]], cdfs[iplus], ecdfs[iplus+1],
...            color='r', linestyle='dashed', lw=4)
>>> plt.show()
../../_images/scipy-special-kolmogorov-1.png
本页内容