scipy.special.

jn_zeros

scipy.special.jn_zeros(n, nt)

计算整数阶贝塞尔函数 Jn 的零点。

在区间 \((0, \infty)\) 上计算贝塞尔函数 \(J_n(x)\) 的 nt 个零点。零点按升序返回。请注意，该区间不包括 \(n > 0\) 时存在的 \(x = 0\) 处的零点。

参数:

nint

贝塞尔函数的阶数

ntint

要返回的零点数

返回值:

ndarray

贝塞尔函数的前 nt 个零点。

另请参阅

jv

第一类实阶贝塞尔函数

jnp_zeros

的零点 \(Jn'\)

参考文献

[1]

Zhang, Shanjie 和 Jin, Jianming。 “特殊函数的计算”，John Wiley and Sons，1996，第 5 章。 https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

示例

在您的浏览器中尝试！

计算 \(J_3\) 的前四个正根。

>>> from scipy.special import jn_zeros
>>> jn_zeros(3, 4)
array([ 6.3801619 ,  9.76102313, 13.01520072, 16.22346616])

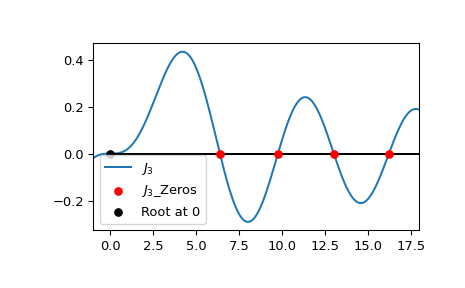
绘制 \(J_3\) 及其前四个正根。请注意，jn_zeros 未返回位于 0 处的根。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import jn, jn_zeros
>>> j3_roots = jn_zeros(3, 4)
>>> xmax = 18
>>> xmin = -1
>>> x = np.linspace(xmin, xmax, 500)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, jn(3, x), label=r'$J_3$')
>>> ax.scatter(j3_roots, np.zeros((4, )), s=30, c='r',
...            label=r"$J_3$_Zeros", zorder=5)
>>> ax.scatter(0, 0, s=30, c='k',
...            label=r"Root at 0", zorder=5)
>>> ax.hlines(0, 0, xmax, color='k')
>>> ax.set_xlim(xmin, xmax)
>>> plt.legend()
>>> plt.show()

返回在新标签页中打开