scipy.special.itairy#
- scipy.special.itairy(x, out=None) = <ufunc 'itairy'>#
艾里函数积分
计算艾里函数从 0 到 x 的积分。
- 参数:
- x类数组
积分上限(浮点数)。
- outnd 数组元组,可选
可选的函数值输出数组
- 返回:
- Apt标量或 nd 数组
Ai(t) 从 0 到 x 的积分。
- Bpt标量或 nd 数组
Bi(t) 从 0 到 x 的积分。
- Ant标量或 nd 数组
Ai(-t) 从 0 到 x 的积分。
- Bnt标量或 nd 数组
Bi(-t) 从 0 到 x 的积分。
说明
由张善杰(Shanjie Zhang)和金建明(Jianming Jin)创建的 Fortran 例程的封装 [1]。
参考文献
[1]Zhang, Shanjie 和 Jin, Jianming. “特殊函数计算”,John Wiley and Sons, 1996. https://people.sc.fsu.edu/~jburkardt/f_src/special_functions/special_functions.html
示例
计算函数在
x=1.处的值。>>> import numpy as np >>> from scipy.special import itairy >>> import matplotlib.pyplot as plt >>> apt, bpt, ant, bnt = itairy(1.) >>> apt, bpt, ant, bnt (0.23631734191710949, 0.8727691167380077, 0.46567398346706845, 0.3730050096342943)
通过为 x 提供 NumPy 数组来计算函数在多个点的值。
>>> x = np.array([1., 1.5, 2.5, 5]) >>> apt, bpt, ant, bnt = itairy(x) >>> apt, bpt, ant, bnt (array([0.23631734, 0.28678675, 0.324638 , 0.33328759]), array([ 0.87276912, 1.62470809, 5.20906691, 321.47831857]), array([0.46567398, 0.72232876, 0.93187776, 0.7178822 ]), array([ 0.37300501, 0.35038814, -0.02812939, 0.15873094]))
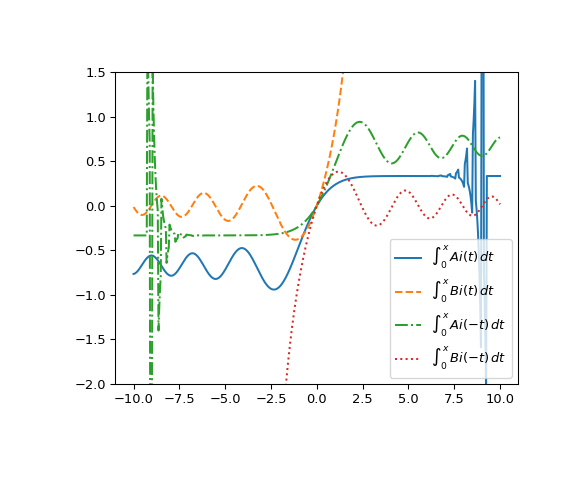
绘制从 -10 到 10 的函数图。
>>> x = np.linspace(-10, 10, 500) >>> apt, bpt, ant, bnt = itairy(x) >>> fig, ax = plt.subplots(figsize=(6, 5)) >>> ax.plot(x, apt, label=r"$\int_0^x\, Ai(t)\, dt$") >>> ax.plot(x, bpt, ls="dashed", label=r"$\int_0^x\, Bi(t)\, dt$") >>> ax.plot(x, ant, ls="dashdot", label=r"$\int_0^x\, Ai(-t)\, dt$") >>> ax.plot(x, bnt, ls="dotted", label=r"$\int_0^x\, Bi(-t)\, dt$") >>> ax.set_ylim(-2, 1.5) >>> ax.legend(loc="lower right") >>> plt.show()