scipy.special.
hermite#
- scipy.special.hermite(n, monic=False)[源代码]#
物理学家埃尔米特多项式。
定义为
\[H_n(x) = (-1)^ne^{x^2}\frac{d^n}{dx^n}e^{-x^2};\]\(H_n\) 是度数为 \(n\) 的多项式。
- 参数:
- nint
多项式的度数。
- monicbool，可选
如果 True，则将前导系数缩放到 1。默认值为 False。
- 返回:
- Horthopoly1d
埃尔米特多项式。
注解
多项式 \(H_n\) 在 \((-\infty, \infty)\) 上正交，权重函数 \(e^{-x^2}\)。
示例
>>> from scipy import special >>> import matplotlib.pyplot as plt >>> import numpy as np
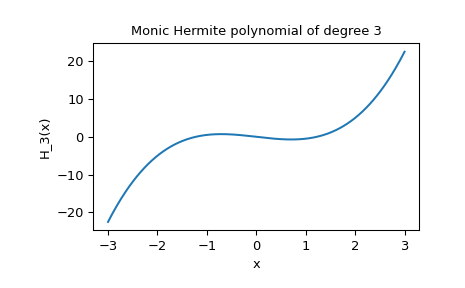
>>> p_monic = special.hermite(3, monic=True) >>> p_monic poly1d([ 1. , 0. , -1.5, 0. ]) >>> p_monic(1) -0.49999999999999983 >>> x = np.linspace(-3, 3, 400) >>> y = p_monic(x) >>> plt.plot(x, y) >>> plt.title("Monic Hermite polynomial of degree 3") >>> plt.xlabel("x") >>> plt.ylabel("H_3(x)") >>> plt.show()
