scipy.special.

diric

scipy.special.diric(x, n)

周期性正弦积分函数，也称为狄利克雷函数。

狄利克雷函数定义为

diric(x, n) = sin(x * n/2) / (n * sin(x / 2)),

其中 n 是正整数。

参数:

x类似数组

输入数据

nint

定义周期性的整数。

返回:

diricndarray

示例

在浏览器中试用它！

>>> import numpy as np
>>> from scipy import special
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-8*np.pi, 8*np.pi, num=201)
>>> plt.figure(figsize=(8, 8));
>>> for idx, n in enumerate([2, 3, 4, 9]):
...     plt.subplot(2, 2, idx+1)
...     plt.plot(x, special.diric(x, n))
...     plt.title('diric, n={}'.format(n))
>>> plt.show()

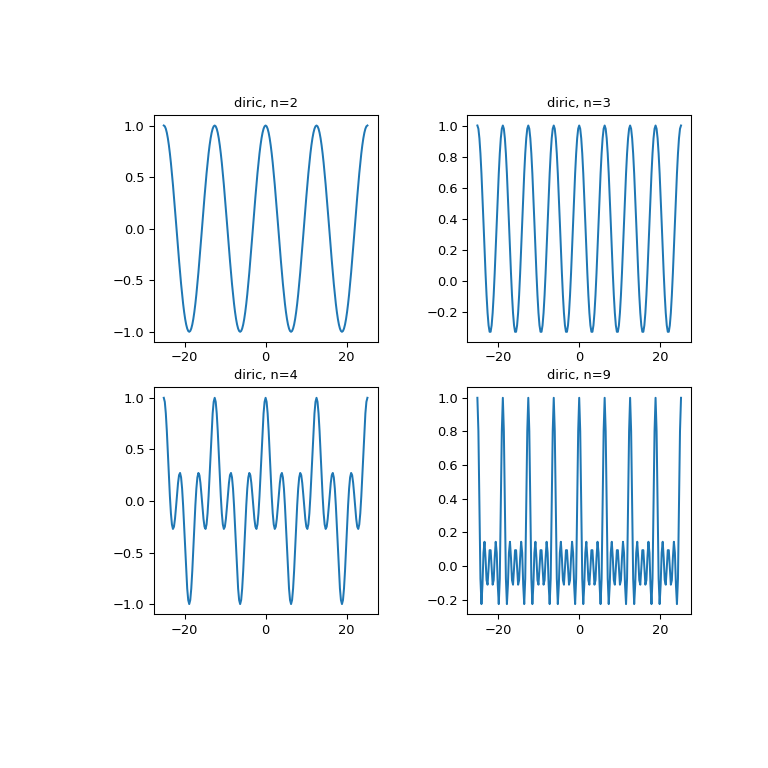
以下示例演示了 diric 给出了矩形脉冲的傅里叶系数的幅度（取模符号和缩放除外）。

抑制有效为 0 的值的输出

>>> np.set_printoptions(suppress=True)

创建一个长度为 m、包含 k 个一的信号 x

>>> m = 8
>>> k = 3
>>> x = np.zeros(m)
>>> x[:k] = 1

使用 FFT 计算 x 的傅里叶变换，并检查系数的幅度

>>> np.abs(np.fft.fft(x))
array([ 3.        ,  2.41421356,  1.        ,  0.41421356,  1.        ,
        0.41421356,  1.        ,  2.41421356])

现在找到相同的（正负）值，使用 diric。我们乘以 k 来平衡 numpy.fft.fft 和 diric 的不同缩放惯例

>>> theta = np.linspace(0, 2*np.pi, m, endpoint=False)
>>> k * special.diric(theta, k)
array([ 3.        ,  2.41421356,  1.        , -0.41421356, -1.        ,
       -0.41421356,  1.        ,  2.41421356])

返回在新选项卡中打开