scipy.signal.

iirnotch#

scipy.signal.iirnotch(w0, Q, fs=2.0)[源代码]#

设计二阶IIR陷波数字滤波器。

陷波滤波器是一种带阻滤波器，具有窄带宽（高品质因数）。它能抑制一个窄频率带，而使频谱的其余部分基本保持不变。

参数:

w0float: 要从信号中移除的频率。如果指定了fs，则其单位与fs相同。默认情况下，它是一个归一化标量，必须满足0 < w0 < 1，其中w0 = 1对应于采样频率的一半。
Qfloat: 品质因数。表征陷波滤波器-3 dB带宽bw相对于其中心频率的无量纲参数，Q = w0/bw。
fsfloat, optional: 数字系统的采样频率。

在 1.2.0 版中新增。

返回:

b, andarray, ndarray: IIR 滤波器的分子（b）和分母（a）多项式。

另请参阅

iirpeak

备注

在 0.19.0 版中新增。

参考文献

[1]

Sophocles J. Orfanidis, “Introduction To Signal Processing”, Prentice-Hall, 1996

示例

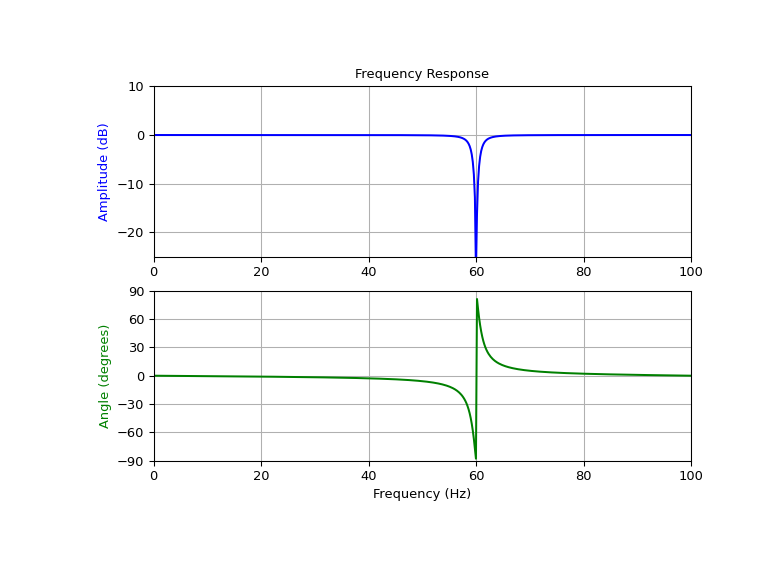
设计并绘制滤波器，以移除从 200 Hz 采样的信号中的 60 Hz 分量，使用品质因数 Q = 30

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> fs = 200.0  # Sample frequency (Hz)
>>> f0 = 60.0  # Frequency to be removed from signal (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design notch filter
>>> b, a = signal.iirnotch(f0, Q, fs)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6))
>>> ax[0].plot(freq, 20*np.log10(abs(h)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude [dB]", color='blue')
>>> ax[0].set_xlim([0, 100])
>>> ax[0].set_ylim([-25, 10])
>>> ax[0].grid(True)
>>> ax[1].plot(freq, np.unwrap(np.angle(h))*180/np.pi, color='green')
>>> ax[1].set_ylabel("Phase [deg]", color='green')
>>> ax[1].set_xlabel("Frequency [Hz]")
>>> ax[1].set_xlim([0, 100])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid(True)
>>> plt.show()

../../_images/scipy-signal-iirnotch-1.png