scipy.signal.

bessel

scipy.signal.bessel(N, Wn, btype='low', analog=False, output='ba', norm='phase', fs=None)

贝塞尔/汤姆逊数字和模拟滤波器设计。

设计一个 N 阶数字或模拟贝塞尔滤波器并返回滤波器系数。

参数:

Nint

滤波器的阶数。

Wnarray_like

一个标量或长度为 2 的序列，给出临界频率（由 norm 参数定义）。对于模拟滤波器，Wn 是角频率（例如，弧度/秒）。

对于数字滤波器，Wn 的单位与 fs 相同。默认情况下，fs 是 2 半周期/样本，因此这些值从 0 到 1 归一化，其中 1 是奈奎斯特频率。（Wn 因此以半周期/样本表示。）

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, 可选

滤波器类型。默认为 'lowpass'。

analogbool, 可选

当为 True 时，返回模拟滤波器，否则返回数字滤波器。（参见注意事项。）

output{‘ba’, ‘zpk’, ‘sos’}, 可选

输出类型：分子/分母（'ba'）、零极点（'zpk'）或二阶截面（'sos'）。默认为 'ba'。

norm{‘phase’, ‘delay’, ‘mag’}, 可选

临界频率归一化

phase

滤波器被归一化，使得相位响应在角频率（例如 弧度/秒）Wn 处达到其中点。这适用于低通和高通滤波器，因此这是“相位匹配”的情况。

幅值响应渐近线与相同阶数、截止频率为 Wn 的巴特沃斯滤波器相同。

这是默认设置，并与 MATLAB 的实现匹配。

delay

滤波器被归一化，使得通带中的群延迟为 1/Wn（例如，秒）。这是通过求解贝塞尔多项式获得的“自然”类型。

mag

滤波器被归一化，使得在角频率 Wn 处的增益幅值为 -3 dB。

在 0.18.0 版本中添加。

fsfloat, 可选

数字系统的采样频率。

在 1.2.0 版本中添加。

返回:

b, andarray, ndarray

IIR 滤波器的分子 (b) 和分母 (a) 多项式。仅当 output='ba' 时返回。

z, p, kndarray, ndarray, float

IIR 滤波器传递函数的零点、极点和系统增益。仅当 output='zpk' 时返回。

sosndarray

IIR 滤波器的二阶截面表示。仅当 output='sos' 时返回。

注意事项

模拟贝塞尔滤波器，也称为汤姆逊滤波器，具有最大平坦的群延迟和最大线性的相位响应，在阶跃响应中几乎没有振铃。 [1]

贝塞尔本身是一种模拟滤波器。此函数使用双线性变换生成数字贝塞尔滤波器，这不保留模拟滤波器的相位响应。因此，它在低于 fs/4 左右的频率下仅近似正确。为了在更高频率下获得最大平坦的群延迟，必须使用相位保持技术对模拟贝塞尔滤波器进行变换。

有关实现细节和参考文献，请参阅 besselap。

'sos' 输出参数在 0.16.0 版本中添加。

参考文献

[1]

Thomson, W.E., “Delay Networks having Maximally Flat Frequency Characteristics”, Proceedings of the Institution of Electrical Engineers, Part III, November 1949, Vol. 96, No. 44, pp. 487-490.

示例

在浏览器中试用！

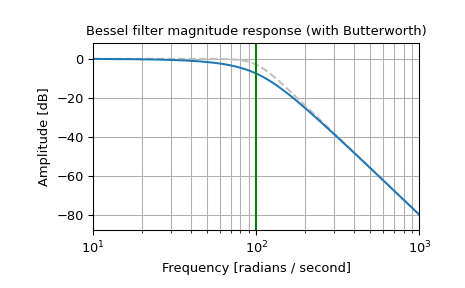
绘制相位归一化频率响应，显示与巴特沃斯截止频率（绿色）的关系

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.butter(4, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)), color='silver', ls='dashed')
>>> b, a = signal.bessel(4, 100, 'low', analog=True, norm='phase')
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)))
>>> plt.title('Bessel filter magnitude response (with Butterworth)')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green')  # cutoff frequency
>>> plt.show()

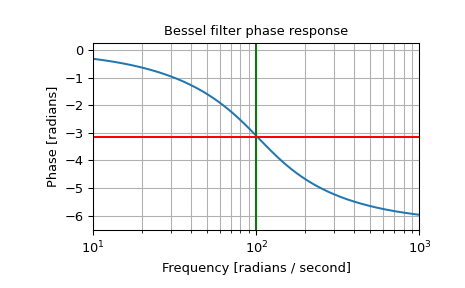
和相位中点

>>> plt.figure()
>>> plt.semilogx(w, np.unwrap(np.angle(h)))
>>> plt.axvline(100, color='green')  # cutoff frequency
>>> plt.axhline(-np.pi, color='red')  # phase midpoint
>>> plt.title('Bessel filter phase response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Phase [rad]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

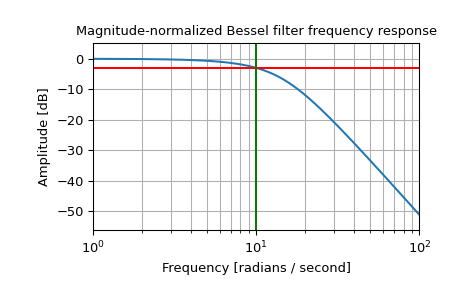
绘制幅值归一化频率响应，显示 -3 dB 截止

>>> b, a = signal.bessel(3, 10, 'low', analog=True, norm='mag')
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)))
>>> plt.axhline(-3, color='red')  # -3 dB magnitude
>>> plt.axvline(10, color='green')  # cutoff frequency
>>> plt.title('Amplitude-normalized Bessel filter frequency response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

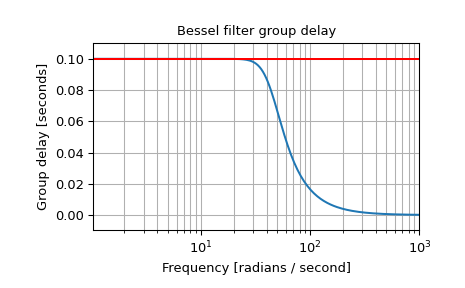
绘制延迟归一化滤波器，显示 0.1 秒处的最大平坦群延迟

>>> b, a = signal.bessel(5, 1/0.1, 'low', analog=True, norm='delay')
>>> w, h = signal.freqs(b, a)
>>> plt.figure()
>>> plt.semilogx(w[1:], -np.diff(np.unwrap(np.angle(h)))/np.diff(w))
>>> plt.axhline(0.1, color='red')  # 0.1 seconds group delay
>>> plt.title('Bessel filter group delay')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Group delay [s]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

返回在新标签页中打开