scipy.interpolate.

lagrange

scipy.interpolate.lagrange(x, w)

返回拉格朗日插值多项式。

给定两个一维数组 x 和 w, 返回通过点 (x, w) 的拉格朗日插值多项式。

警告：此实现存在数值不稳定问题。即使点选择最优，也不要期望能够使用超过大约 20 个点。

参数:

x类数组

x 表示一组数据点的 x 坐标。

w类数组

w 表示一组数据点的 y 坐标，即 f(x)。

返回:

lagrangenumpy.poly1d 实例

拉格朗日插值多项式。

注意

此函数的名称是指返回的对象代表一个拉格朗日多项式，它是插值给定数据集的最低次唯一多项式 [1]。它使用牛顿的差商公式 [2] 计算多项式；也就是说，它使用牛顿基多项式而不是拉格朗日基多项式。对于数值计算，拉格朗日插值的重心形式 (scipy.interpolate.BarycentricInterpolator) 通常更合适。

参考

[1]

拉格朗日多项式。维基百科。 https://en.wikipedia.org/wiki/Lagrange_polynomial

[2]

牛顿多项式。维基百科。 https://en.wikipedia.org/wiki/Newton_polynomial

示例

在浏览器中尝试！

使用 3 个点插值 \(f(x) = x^3\)。

>>> import numpy as np
>>> from scipy.interpolate import lagrange
>>> x = np.array([0, 1, 2])
>>> y = x**3
>>> poly = lagrange(x, y)

由于只有 3 个点，拉格朗日多项式的次数为 2。具体地，它由以下公式给出：

\[\begin{split}\begin{aligned} L(x) &= 1\times \frac{x (x - 2)}{-1} + 8\times \frac{x (x-1)}{2} \\ &= x (-2 + 3x) \end{aligned}\end{split}\]

>>> from numpy.polynomial.polynomial import Polynomial
>>> Polynomial(poly.coef[::-1]).coef
array([ 0., -2.,  3.])

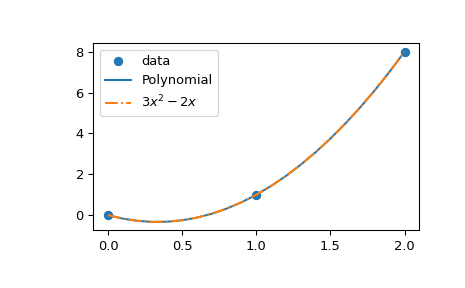
>>> import matplotlib.pyplot as plt
>>> x_new = np.arange(0, 2.1, 0.1)
>>> plt.scatter(x, y, label='data')
>>> plt.plot(x_new, Polynomial(poly.coef[::-1])(x_new), label='Polynomial')
>>> plt.plot(x_new, 3*x_new**2 - 2*x_new + 0*x_new,
...          label=r"$3 x^2 - 2 x$", linestyle='-.')
>>> plt.legend()
>>> plt.show()

返回在新标签页中打开