scipy.interpolate.

approximate_taylor_polynomial

scipy.interpolate.approximate_taylor_polynomial(f, x, degree, scale, order=None)

通过多项式拟合估计 f 在 x 处的泰勒多项式。

参数:

f可调用对象

目标泰勒多项式的函数。应该接受一个 x 值向量。

x标量

多项式将被计算的点。

degree整数

泰勒多项式的阶数

scale标量

用于评估泰勒多项式的区间宽度。此宽度范围内分布的函数值用于拟合多项式。必须谨慎选择。

order整数或None，可选

用于拟合的多项式阶数；f 将被评估 order+1 次。如果为 None，则使用 degree。

返回:

ppoly1d 实例

泰勒多项式（平移到原点，例如 p(0)=f(x)）。

注意

“scale”的适当选择是一种权衡；过大时，函数与其泰勒多项式相差过大，无法得到好的结果；过小时，舍入误差会淹没高阶项。即使在理想情况下，所用算法在阶数约为 30 时也会变得数值不稳定。

选择略大于 degree 的 order 可能会改善高阶项。

示例

在浏览器中试用！

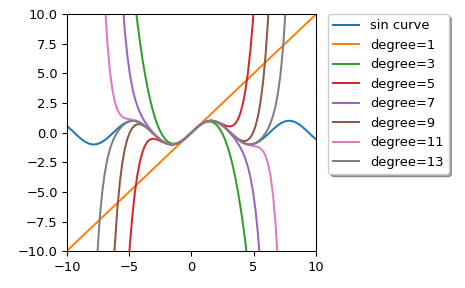
我们可以计算不同阶数的 sin 函数的泰勒近似多项式

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import approximate_taylor_polynomial
>>> x = np.linspace(-10.0, 10.0, num=100)
>>> plt.plot(x, np.sin(x), label="sin curve")
>>> for degree in np.arange(1, 15, step=2):
...     sin_taylor = approximate_taylor_polynomial(np.sin, 0, degree, 1,
...                                                order=degree + 2)
...     plt.plot(x, sin_taylor(x), label=f"degree={degree}")
>>> plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left',
...            borderaxespad=0.0, shadow=True)
>>> plt.tight_layout()
>>> plt.axis([-10, 10, -10, 10])
>>> plt.show()

返回在新标签页中打开