scipy.stats.

truncate

scipy.stats.truncate(X, lb=-inf, ub=inf)

截断随机变量的支持域。

给定一个随机变量 X, truncate 返回一个随机变量，其支持域被截断到 lb 和 ub 之间的区间。 相应的概率密度函数会被归一化。

参数:

XContinuousDistribution

要截断的随机变量。

lb, ubfloat 数组型

下限和上限截断点，分别。 必须彼此和 X 的形状进行广播。

返回:

XContinuousDistribution

被截断的随机变量。

参考文献

[1]

“截断分布”。 Wikipedia. https://en.wikipedia.org/wiki/Truncated_distribution

示例

在您的浏览器中尝试！

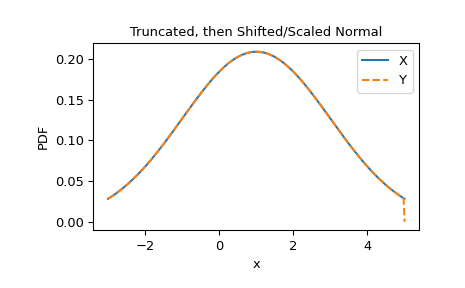
与 scipy.stats.truncnorm 比较，它截断一个标准正态分布，然后平移和缩放它。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> loc, scale, lb, ub = 1, 2, -2, 2
>>> X = stats.truncnorm(lb, ub, loc, scale)
>>> Y = scale * stats.truncate(stats.Normal(), lb, ub) + loc
>>> x = np.linspace(-3, 5, 300)
>>> plt.plot(x, X.pdf(x), '-', label='X')
>>> plt.plot(x, Y.pdf(x), '--', label='Y')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF')
>>> plt.title('Truncated, then Shifted/Scaled Normal')
>>> plt.legend()
>>> plt.show()

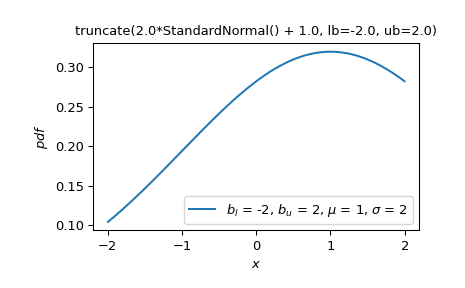
但是，假设我们希望平移和缩放一个正态随机变量，然后将其支持域截断为给定的值。 使用 truncate 这是很简单的。

>>> Z = stats.truncate(scale * stats.Normal() + loc, lb, ub)
>>> Z.plot()
>>> plt.show()

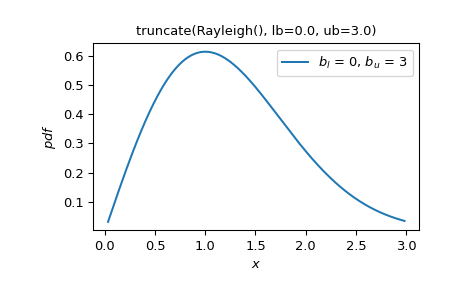
此外，truncate 可以应用于任何随机变量

>>> Rayleigh = stats.make_distribution(stats.rayleigh)
>>> W = stats.truncate(Rayleigh(), lb=0.5, ub=3)
>>> W.plot()
>>> plt.show()

返回在新标签页中打开