scipy.stats.
order_statistic#
- scipy.stats.order_statistic(X, /, *, r, n)[source]#
顺序统计量的概率分布
返回一个随机变量,该变量遵循随机变量 \(X\) 的 \(n\) 个观测值的样本的 \(r^{\text{th}}\) 顺序统计量背后的分布。
- 参数:
- XContinuousDistribution
随机变量 \(X\)
- rarray_like
顺序统计量 \(r\) 的 (正整数) 秩
- narray_like
(正整数) 样本大小 \(n\)
- 返回:
- YContinuousDistribution
一个随机变量,它遵循规定的顺序统计量的分布。
注释
如果我们对连续随机变量 \(X\) 进行 \(n\) 次观测,并按递增顺序排序 \(X_{(1)}, \dots, X_{(r)}, \dots, X_{(n)}\),则 \(X_{(r)}\) 被称为 \(r^{\text{th}}\) 顺序统计量。
如果 math:X 的 PDF、CDF 和 CCDF 分别表示为 \(f\)、\(F\) 和 \(F'\),那么 math:X_{(r)} 的 PDF 由下式给出
\[f_r(x) = \frac{n!}{(r-1)! (n-r)!} f(x) F(x)^{r-1} F'(x)^{n - r}\]分布基础 \(X_{(r)}\) 的 CDF 和其他方法是使用 \(X = F^{-1}(U)\) 这一事实计算的,其中 \(U\) 是标准均匀随机变量,并且 U 的观测值的顺序统计量遵循 beta 分布 \(B(r, n - r + 1)\)。
参考文献
[1]顺序统计量。 维基百科。 https://en.wikipedia.org/wiki/Order_statistic
示例
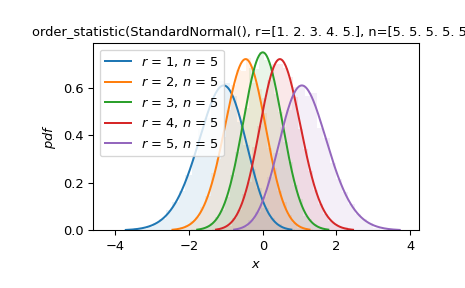
假设我们对从标准正态分布中抽取的五个大小的样本的顺序统计量感兴趣。 绘制每个顺序统计量的 PDF 并与模拟的归一化直方图进行比较。
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy import stats >>> >>> X = stats.Normal() >>> data = X.sample(shape=(10000, 5)) >>> sorted = np.sort(data, axis=1) >>> Y = stats.order_statistic(X, r=[1, 2, 3, 4, 5], n=5) >>> >>> ax = plt.gca() >>> colors = plt.rcParams['axes.prop_cycle'].by_key()['color'] >>> for i in range(5): ... y = sorted[:, i] ... ax.hist(y, density=True, bins=30, alpha=0.1, color=colors[i]) >>> Y.plot(ax=ax) >>> plt.show()