scipy.stats.sampling.

NumericalInversePolynomial

class scipy.stats.sampling.NumericalInversePolynomial(dist, *, mode=None, center=None, domain=None, order=5, u_resolution=1e-10, random_state=None)

基于多项式插值的CDF反演（PINV）。

PINV是数值反演的一种变体，其中使用牛顿插值公式逼近逆CDF。区间 [0,1] 被分割成几个子区间。在每个子区间中，逆CDF在节点 (CDF(x),x) 处针对子区间中的某些点 x 构建。如果给定了PDF，则使用具有 5 个点的自适应 Gauss-Lobatto 积分，从给定的 PDF 数值计算 CDF。子区间会被分割，直到达到请求的精度目标。

该方法不是精确的，因为它只产生近似分布的随机变量。 然而，最大容忍的近似误差可以设置为分辨率（当然，受机器精度的限制）。我们使用 u 误差 |U - CDF(X)| 来测量误差，其中 X 是对应于分位数 U 的近似百分位数，即 X = approx_ppf(U)。我们称最大容忍的 u 误差为算法的 u 分辨率。

可以同时选择插值多项式的阶数和 u 分辨率。请注意，非常小的 u 分辨率值是可能的，但会增加设置步骤的成本。

必须在设置步骤中计算插值多项式。然而，它只适用于具有有界域的分布；对于具有无界域的分布，尾部被截断，使得尾部区域的概率与给定的 u 分辨率相比很小。

只有当PDF是单峰的或当PDF在两个模式之间不消失时，插值多项式的构造才有效。

对于给定的分布有一些限制

• 分布的支持（即 PDF 严格为正的区域）必须是连通的。 实际上，这意味着 PDF “不太小”的区域必须是连通的。 单峰密度满足此条件。 如果违反此条件，则可能会截断分布的域。

• 当 PDF 以数值方式积分时，给定的 PDF 必须是连续的并且应该是平滑的。

• PDF 必须是有界的。

• 当分布具有重尾（因为逆CDF在0或1处变得非常陡峭）并且请求的 u 分辨率非常小时，该算法会出现问题。 例如，当请求的 u 分辨率小于 1.e-12 时，柯西分布很可能会显示此问题。

参数:

distobject

具有 pdf 或 logpdf 方法的类的实例，可以选择具有 cdf 方法。

• pdf: 分布的PDF。 PDF的签名应为：def pdf(self, x: float) -> float，即PDF应接受Python浮点数并返回Python浮点数。它不需要积分为1，即PDF不需要归一化。此方法是可选的，但需要指定 pdf 或 logpdf 之一。如果两者都给出，则使用 logpdf。

• logpdf: 分布的PDF的对数。签名与 pdf 的签名相同。 同样，PDF的归一化常数的对数可以忽略。此方法是可选的，但需要指定 pdf 或 logpdf 之一。如果两者都给出，则使用 logpdf。

• cdf: 分布的CDF。 此方法是可选的。如果提供，则可以计算“u-error”。请参阅 u_error。必须与 PDF 具有相同的签名。

modefloat, optional

分布的（精确）模式。 默认为 None。

centerfloat, optional

分布的模式或平均值的近似位置。 此位置提供有关PDF主要部分的一些信息，并用于避免数值问题。 默认为 None。

domainlist or tuple of length 2, optional

分布的支持。 默认为 None。 当 None

• 如果分布对象 dist 提供了 support 方法，则它用于设置分布的域。

• 否则，假定支持为 \((-\infty, \infty)\)。

orderint, optional

插值多项式的阶数。 有效的阶数介于 3 和 17 之间。阶数越高，近似值的间隔越少。 默认为 5。

u_resolutionfloat, optional

设置最大容忍的 u-error。 u_resolution 的值必须至少为 1.e-15，最多为 1.e-5。 请注意，大多数均匀随机数源的分辨率为 2-32= 2.3e-10。 因此，1.e-10 的值会导致一种可以称为精确的反演算法。 对于大多数模拟，最大误差的稍微大一点的值也足够了。 默认为 1e-10。

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState}, optional

用于生成均匀随机数流的底层 NumPy 随机数生成器或种子。 如果 random_state 为 None（或 np.random），则使用 numpy.random.RandomState 单例。 如果 random_state 是一个 int，则使用一个新的 RandomState 实例，并以 random_state 为种子。 如果 random_state 已经是 Generator 或 RandomState 实例，则使用该实例。

属性:

intervals

获取计算中使用的间隔数。

方法

cdf(x)	给定分布的近似累积分布函数。
ppf(u)	给定分布的近似PPF。
qrvs([size, d, qmc_engine])	给定RV的准随机变量。
rvs([size, random_state])	从分布中抽样。
set_random_state([random_state])	设置底层均匀随机数生成器。
u_error([sample_size])	使用蒙特卡罗模拟估计近似值的 u 误差。

参考文献

[1]

Derflinger, Gerhard, Wolfgang Hörmann, and Josef Leydold. “Random variate generation by numerical inversion when only the density is known.” ACM Transactions on Modeling and Computer Simulation (TOMACS) 20.4 (2010): 1-25.

[2]

UNU.RAN 参考手册，第 5.3.12 节，“PINV - 基于多项式插值的CDF反演”，https://statmath.wu.ac.at/software/unuran/doc/unuran.html#PINV

例子

在您的浏览器中尝试一下！

>>> from scipy.stats.sampling import NumericalInversePolynomial
>>> from scipy.stats import norm
>>> import numpy as np

要创建一个从标准正态分布中抽样的生成器，请执行以下操作

>>> class StandardNormal:
...    def pdf(self, x):
...        return np.exp(-0.5 * x*x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)

创建生成器后，可以通过调用 rvs 方法从分布中抽取样本

>>> rng.rvs()
-1.5244996276336318

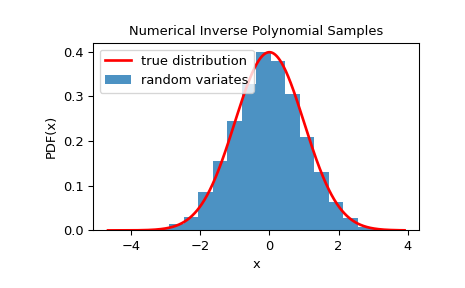
为了检查随机变量是否紧密跟随给定的分布，我们可以查看它的直方图

>>> import matplotlib.pyplot as plt
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Numerical Inverse Polynomial Samples')
>>> plt.legend()
>>> plt.show()

如果在设置期间可以使用精确的CDF，则可以估计近似PPF的 u 误差。 为此，在初始化期间传递一个具有分布的精确CDF的 dist 对象

>>> from scipy.special import ndtr
>>> class StandardNormal:
...    def pdf(self, x):
...        return np.exp(-0.5 * x*x)
...    def cdf(self, x):
...        return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)

现在，可以通过调用 u_error 方法来估计 u 误差。 它运行蒙特卡罗模拟来估计 u 误差。 默认情况下，使用 100000 个样本。 要更改此设置，可以将样本数作为参数传递

>>> rng.u_error(sample_size=1000000)  # uses one million samples
UError(max_error=8.785994154436594e-11, mean_absolute_error=2.930890027826552e-11)

这将返回一个 namedtuple，其中包含最大 u 误差和平均绝对 u 误差。

可以通过降低 u 分辨率（最大允许的 u 误差）来降低 u 误差

>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, u_resolution=1.e-12, random_state=urng)
>>> rng.u_error(sample_size=1000000)
UError(max_error=9.07496300328603e-13, mean_absolute_error=3.5255644517257716e-13)

请注意，这会增加设置时间。

可以通过调用 ppf 方法来评估近似PPF

>>> rng.ppf(0.975)
1.9599639857012559
>>> norm.ppf(0.975)
1.959963984540054

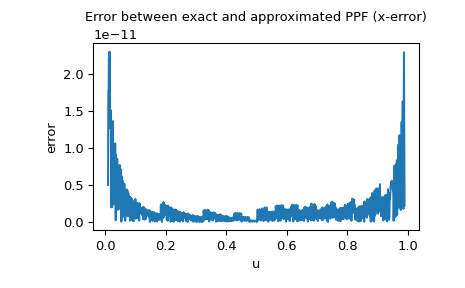
由于正态分布的PPF可以作为特殊函数使用，因此我们还可以检查 x 误差，即近似PPF和精确PPF之间的差异

>>> import matplotlib.pyplot as plt
>>> u = np.linspace(0.01, 0.99, 1000)
>>> approxppf = rng.ppf(u)
>>> exactppf = norm.ppf(u)
>>> error = np.abs(exactppf - approxppf)
>>> plt.plot(u, error)
>>> plt.xlabel('u')
>>> plt.ylabel('error')
>>> plt.title('Error between exact and approximated PPF (x-error)')
>>> plt.show()

返回在新标签页中打开