scipy.stats.sampling.

NumericalInverseHermite#

class scipy.stats.sampling.NumericalInverseHermite(dist, *, domain=None, order=3, u_resolution=1e-12, construction_points=None, random_state=None)#

基于 Hermite 插值的 CDF 逆函数 (HINV)。

HINV 是数值逆函数的一种变体，其中逆 CDF 使用 Hermite 插值来近似，即，区间 [0,1] 被分割成几个区间，并且在每个区间中，逆 CDF 由通过 CDF 和 PDF 在区间边界处的值构造的多项式来近似。这使得可以通过分割特定区间来提高精度，而无需在未受影响的区间中重新计算。实现了三种类型的样条曲线：线性、三次和五次插值。对于线性插值，只需要 CDF。三次插值还需要 PDF，而五次插值需要 PDF 及其导数。

这些样条曲线必须在设置步骤中计算。但是，它仅适用于具有有界域的分布；对于具有无界域的分布，尾部被截断，使得尾部区域的概率与给定的 u 分辨率相比很小。

该方法不是精确的，因为它仅生成近似分布的随机变量。然而，在 “u 方向” 上的最大数值误差 (即 |U - CDF(X)| 其中 X 是对应于分位数 U 的近似百分位数，即 X = approx_ppf(U)) 可以设置为所需的分辨率 (在机器精度范围内)。请注意，非常小的 u 分辨率值是可能的，但可能会增加设置步骤的成本。

参数:

dist对象

具有 cdf 并且可以选择具有 pdf 和 dpdf 方法的类的实例。

cdf: 分布的 CDF。CDF 的签名应为: def cdf(self, x: float) -> float。即 CDF 应该接受一个 Python float 并返回一个 Python float。
pdf: 分布的 PDF。当 order=1 时，此方法是可选的。必须与 CDF 具有相同的签名。
dpdf: PDF 关于变量的导数 (即 x)。当 order=1 或 order=3 时，此方法是可选的。必须与 CDF 具有相同的签名。

domain长度为 2 的列表或元组，可选

分布的支持。默认为 None。当 None 时

如果分布对象 *dist* 提供了 support 方法，则它用于设置分布的域。
否则，假定支持为 \((-\infty, \infty)\)。

orderint, 默认值: 3

设置 Hermite 插值的阶数。有效的阶数为 1、3 和 5。有效的阶数为 1、3 和 5。请注意，大于 1 的阶数需要分布的密度，而大于 3 的阶数甚至需要密度的导数。使用 1 阶会导致大多数分布中出现大量的区间，因此不建议使用。如果 u 方向的最大误差非常小 (比如小于 1.e-10)，建议使用 5 阶，因为它会导致更少的设计点，只要没有极点或重尾。

u_resolutionfloat, 默认值: 1e-12

设置最大容许的 u 误差。请注意，大多数均匀随机数源的分辨率为 2-32= 2.3e-10。因此，1.e-10 的值会导致一种可以称为精确的反演算法。对于大多数模拟，略大的最大误差值也足够了。默认值为 1e-12。

construction_pointsarray_like, 可选

设置 Hermite 插值的起始构造点 (节点)。由于可能的最大误差仅在设置中估计，因此可能需要设置一些特殊的设计点来计算 Hermite 插值，以保证最大 u 误差不会大于所需值。此类点是密度不可微或具有局部极值的点。

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState}, 可选

用于生成均匀随机数流的底层 NumPy 随机数生成器或种子。如果 *random_state* 为 None (或 *np.random*)，则使用 numpy.random.RandomState 单例。如果 *random_state* 是一个 int，则使用一个新的 RandomState 实例，并使用 *random_state* 作为种子。如果 *random_state* 已经是一个 Generator 或 RandomState 实例，则使用该实例。

属性:

intervals: 获取生成器对象中用于 Hermite 插值的节点 (设计点) 数。
midpoint_error

方法

`ppf`(u)	给定分布的近似 PPF。
`qrvs`([size, d, qmc_engine])	给定 RV 的准随机变量。
`rvs`([size, random_state])	从分布中采样。
`set_random_state`([random_state])	设置底层均匀随机数生成器。
`u_error`([sample_size])	使用蒙特卡罗模拟估计近似的 u 误差。

注意

NumericalInverseHermite 使用 Hermite 样条近似连续统计分布的 CDF 的逆函数。可以通过传递 *order* 参数来指定 Hermite 样条的阶数。

如 [1] 中所述，它首先通过在分布支持范围内的分位数网格 x 处评估分布的 PDF 和 CDF 来开始。它使用结果来拟合 Hermite 样条 H，使得 H(p) == x，其中 p 是与分位数 x 对应的百分位数数组。因此，样条在百分位数 p 处以机器精度近似分布的 CDF 的逆函数，但通常，样条在百分位数点之间的中点处的精度不会那么高。

p_mid = (p[:-1] + p[1:])/2

因此，需要细化分位数网格以减少最大 “u 误差”

u_error = np.max(np.abs(dist.cdf(H(p_mid)) - p_mid))

低于指定的容差 *u_resolution*。当达到所需的容差或下次细化后的网格区间数可能超过最大允许的区间数 (100000) 时，细化停止。

参考文献

[1]

Hörmann, Wolfgang, and Josef Leydold. “Continuous random variate generation by fast numerical inversion.” ACM Transactions on Modeling and Computer Simulation (TOMACS) 13.4 (2003): 347-362.

[2]

UNU.RAN 参考手册，第 5.3.5 节，“HINV - 基于 Hermite 插值的 CDF 逆函数”，https://statmath.wu.ac.at/software/unuran/doc/unuran.html#HINV

示例

>>> from scipy.stats.sampling import NumericalInverseHermite
>>> from scipy.stats import norm, genexpon
>>> from scipy.special import ndtr
>>> import numpy as np

要创建一个从标准正态分布中采样的生成器，请执行以下操作

>>> class StandardNormal:
...     def pdf(self, x):
...        return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
...     def cdf(self, x):
...        return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, random_state=urng)

NumericalInverseHermite 有一个近似分布的 PPF 的方法。

>>> rng = NumericalInverseHermite(dist)
>>> p = np.linspace(0.01, 0.99, 99) # percentiles from 1% to 99%
>>> np.allclose(rng.ppf(p), norm.ppf(p))
True

根据分布的随机采样方法的实现，在给定相同随机状态的情况下，生成的随机变量可能几乎相同。

>>> dist = genexpon(9, 16, 3)
>>> rng = NumericalInverseHermite(dist)
>>> # `seed` ensures identical random streams are used by each `rvs` method
>>> seed = 500072020
>>> rvs1 = dist.rvs(size=100, random_state=np.random.default_rng(seed))
>>> rvs2 = rng.rvs(size=100, random_state=np.random.default_rng(seed))
>>> np.allclose(rvs1, rvs2)
True

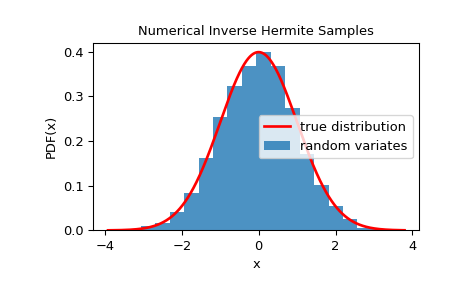
为了检查随机变量是否紧密遵循给定的分布，我们可以查看其直方图

>>> import matplotlib.pyplot as plt
>>> dist = StandardNormal()
>>> rng = NumericalInverseHermite(dist)
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Numerical Inverse Hermite Samples')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-stats-sampling-NumericalInverseHermite-1_00_00.png

给定 PDF 关于变量的导数 (即 x)，我们可以使用五次 Hermite 插值通过传递 *order* 参数来近似 PPF

>>> class StandardNormal:
...     def pdf(self, x):
...        return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
...     def dpdf(self, x):
...        return -1/np.sqrt(2*np.pi) * x * np.exp(-x**2 / 2)
...     def cdf(self, x):
...        return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, order=5, random_state=urng)

阶数越高，区间数越少

>>> rng3 = NumericalInverseHermite(dist, order=3)
>>> rng5 = NumericalInverseHermite(dist, order=5)
>>> rng3.intervals, rng5.intervals
(3000, 522)

可以通过调用 u_error 方法来估计 u 误差。它运行一个小的蒙特卡罗模拟来估计 u 误差。默认情况下，使用 100,000 个样本。可以通过传递 *sample_size* 参数来更改此值

>>> rng1 = NumericalInverseHermite(dist, u_resolution=1e-10)
>>> rng1.u_error(sample_size=1000000)  # uses one million samples
UError(max_error=9.53167544892608e-11, mean_absolute_error=2.2450136432146864e-11)

这将返回一个 namedtuple，其中包含最大 u 误差和平均绝对 u 误差。

可以通过降低 u 分辨率 (最大允许 u 误差) 来减少 u 误差

>>> rng2 = NumericalInverseHermite(dist, u_resolution=1e-13)
>>> rng2.u_error(sample_size=1000000)
UError(max_error=9.32027892364129e-14, mean_absolute_error=1.5194172675685075e-14)

请注意，这会增加设置时间和区间数。

>>> rng1.intervals
1022
>>> rng2.intervals
5687
>>> from timeit import timeit
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-10)
>>> timeit(f, number=1)
0.017409582000254886  # may vary
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-13)
>>> timeit(f, number=1)
0.08671202100003939  # may vary

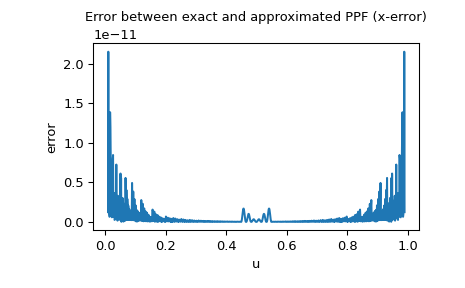
由于正态分布的 PPF 可以作为特殊函数使用，我们还可以检查 x 误差，即近似 PPF 和精确 PPF 之间的差异

>>> import matplotlib.pyplot as plt
>>> u = np.linspace(0.01, 0.99, 1000)
>>> approxppf = rng.ppf(u)
>>> exactppf = norm.ppf(u)
>>> error = np.abs(exactppf - approxppf)
>>> plt.plot(u, error)
>>> plt.xlabel('u')
>>> plt.ylabel('error')
>>> plt.title('Error between exact and approximated PPF (x-error)')
>>> plt.show()

../../_images/scipy-stats-sampling-NumericalInverseHermite-1_01_00.png