differential_entropy#
- scipy.stats.differential_entropy(values, *, window_length=None, base=None, axis=0, method='auto', nan_policy='propagate', keepdims=False)[source]#
给定分布的样本,估计微分熵。
可以使用 method 参数使用几种估计方法。 默认情况下,会根据样本的大小选择一种方法。
- 参数:
- values序列
来自连续分布的样本。
- window_lengthint,可选
用于计算 Vasicek 估计的窗口长度。 必须是介于 1 和样本大小一半之间的整数。 如果
None(默认),它使用启发式值\[\left \lfloor \sqrt{n} + 0.5 \right \rfloor\]其中 \(n\) 是样本大小。 此启发式方法最初在 [2] 中提出,并且已在文献中变得常见。
- basefloat,可选
要使用的对数基数,默认为
e(自然对数)。- axisint 或 None,默认值:0
如果为 int,则输入轴,沿该轴计算统计信息。 输入的每个轴切片(例如,行)的统计信息将显示在输出的相应元素中。 如果
None,则将在计算统计信息之前将输入展平。- method{‘vasicek’, ‘van es’, ‘ebrahimi’, ‘correa’, ‘auto’},可选
用于从样本估计微分熵的方法。 默认值为
'auto'。 有关更多信息,请参见“注释”。- nan_policy{‘propagate’, ‘omit’, ‘raise’}
定义如何处理输入 NaN。
propagate:如果 NaN 存在于计算统计信息的轴切片(例如,行)中,则输出的相应条目将为 NaN。omit:执行计算时将忽略 NaN。 如果沿计算统计信息的轴切片中剩余的数据不足,则输出的相应条目将为 NaN。raise:如果存在 NaN,将引发ValueError。
- keepdimsbool,默认值:False
如果将其设置为 True,则缩减的轴将保留在结果中,作为大小为 1 的维度。 使用此选项,结果将正确地广播到输入数组。
- 返回:
- entropyfloat
计算出的微分熵。
注释
此函数将在极限中收敛到真正的微分熵
\[n \to \infty, \quad m \to \infty, \quad \frac{m}{n} \to 0\]给定样本大小的最佳
window_length选择取决于(未知)分布。 通常,分布的密度越平滑,window_length的最佳值越大 [1]。以下选项可用于 method 参数。
'vasicek'使用 [1] 中介绍的估计器。 这是微分熵的第一个也是最有影响力的估计器之一。'van es'使用 [3] 中提供的偏差校正估计器,该估计器不仅一致,而且在某些条件下是渐近正态的。'ebrahimi'使用 [4] 中提供的估计器,该估计器在模拟中显示出比 Vasicek 估计器更小的偏差和均方误差。'correa'使用 [5] 中提供的基于局部线性回归的估计器。 在一项模拟研究中,它始终具有比 Vasiceck 估计器更小的均方误差,但计算成本更高。'auto'自动选择方法(默认)。 目前,对于非常小的样本(<10),它选择'van es',对于中等样本大小(11-1000),它选择'ebrahimi',对于较大的样本,它选择'vasicek',但此行为可能会在未来版本中发生更改。
所有估计器均按照 [6] 中的描述实现。
从 SciPy 1.9 开始,
np.matrix输入(不建议用于新代码)在执行计算之前会转换为np.ndarray。 在这种情况下,输出将是标量或适当形状的np.ndarray,而不是 2Dnp.matrix。 同样,虽然会忽略屏蔽数组的屏蔽元素,但输出将是标量或np.ndarray,而不是mask=False的屏蔽数组。参考文献
[1] (1,2)Vasicek, O. (1976). A test for normality based on sample entropy. Journal of the Royal Statistical Society: Series B (Methodological), 38(1), 54-59.
[2]Crzcgorzewski, P., & Wirczorkowski, R. (1999). Entropy-based goodness-of-fit test for exponentiality. Communications in Statistics-Theory and Methods, 28(5), 1183-1202.
[3]Van Es, B. (1992). Estimating functionals related to a density by a class of statistics based on spacings. Scandinavian Journal of Statistics, 61-72.
[4]Ebrahimi, N., Pflughoeft, K., & Soofi, E. S. (1994). Two measures of sample entropy. Statistics & Probability Letters, 20(3), 225-234.
[5]Correa, J. C. (1995). A new estimator of entropy. Communications in Statistics-Theory and Methods, 24(10), 2439-2449.
[6]Noughabi, H. A. (2015). Entropy Estimation Using Numerical Methods. Annals of Data Science, 2(2), 231-241. https://link.springer.com/article/10.1007/s40745-015-0045-9
示例
>>> import numpy as np >>> from scipy.stats import differential_entropy, norm
标准正态分布的熵
>>> rng = np.random.default_rng() >>> values = rng.standard_normal(100) >>> differential_entropy(values) 1.3407817436640392
与真实熵进行比较
>>> float(norm.entropy()) 1.4189385332046727
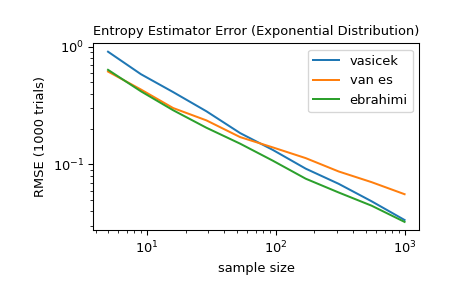
对于 5 到 1000 之间的多个样本大小,比较
'vasicek'、'van es'和'ebrahimi'方法的准确性。 具体来说,比较估计值与分布的真实微分熵之间的均方根误差(超过 1000 次试验)。>>> from scipy import stats >>> import matplotlib.pyplot as plt >>> >>> >>> def rmse(res, expected): ... '''Root mean squared error''' ... return np.sqrt(np.mean((res - expected)**2)) >>> >>> >>> a, b = np.log10(5), np.log10(1000) >>> ns = np.round(np.logspace(a, b, 10)).astype(int) >>> reps = 1000 # number of repetitions for each sample size >>> expected = stats.expon.entropy() >>> >>> method_errors = {'vasicek': [], 'van es': [], 'ebrahimi': []} >>> for method in method_errors: ... for n in ns: ... rvs = stats.expon.rvs(size=(reps, n), random_state=rng) ... res = stats.differential_entropy(rvs, method=method, axis=-1) ... error = rmse(res, expected) ... method_errors[method].append(error) >>> >>> for method, errors in method_errors.items(): ... plt.loglog(ns, errors, label=method) >>> >>> plt.legend() >>> plt.xlabel('sample size') >>> plt.ylabel('RMSE (1000 trials)') >>> plt.title('Entropy Estimator Error (Exponential Distribution)')