scipy.stats.

binned_statistic

scipy.stats.binned_statistic(x, values, statistic='mean', bins=10, range=None)

为一组或多组数据计算分箱统计量。

这是直方图函数的推广。直方图将空间划分为多个箱子，并返回每个箱子中点的数量计数。此函数允许计算每个箱子内值的总和、平均值、中位数或其他统计量（或一组值）。

参数:

x(N,) 类数组

要分箱的值序列。

values(N,) 类数组 或 (N,) 类数组列表

将在其上计算统计量的数据。其形状必须与 x 相同，或是一组序列，每个序列的形状与 x 相同。如果 values 是一组序列，则将独立计算每个序列的统计量。

statistic字符串或可调用对象，可选

要计算的统计量（默认为“mean”）。可以使用以下统计量

• “mean”：计算每个箱子内点的平均值。空箱子将用 NaN 表示。

• “std”：计算每个箱子内的标准差。这是隐式地使用 ddof=0 计算的。

• “median”：计算每个箱子内点的中位数。空箱子将用 NaN 表示。

• “count”：计算每个箱子内的点数。这与未加权的直方图相同。不引用 values 数组。

• “sum”：计算每个箱子内点的总和。这与加权直方图相同。

• “min”：计算每个箱子内点的最小值。空箱子将用 NaN 表示。

• “max”：计算每个箱子内点的最大值。空箱子将用 NaN 表示。

• 函数：一个用户定义的函数，它接受一个值的 1D 数组，并输出一个数值统计量。此函数将在每个箱子中的值上调用。空箱子将用 function([]) 表示，如果此函数返回错误，则用 NaN 表示。

bins整数或标量序列，可选

如果 bins 是一个整数，则它定义给定范围内的等宽箱子的数量（默认为 10）。如果 bins 是一个序列，则它定义箱子的边缘，包括最右边的边缘，允许不均匀的箱子宽度。x 中小于最低箱子边缘的值将分配给箱子编号 0，超出最高箱子的值将分配给 bins[-1]。如果指定了箱子边缘，则箱子的数量将为 (nx = len(bins)-1)。

range(浮点数, 浮点数) 或 [(浮点数, 浮点数)]，可选

箱子的下限和上限范围。如果未提供，则范围默认为 (x.min(), x.max())。超出范围的值将被忽略。

返回:

statistic数组

每个箱子中选定统计量的值。

bin_edges浮点数类型的数组

返回箱子边缘 (length(statistic)+1)。

binnumber：整数的一维 ndarray

每个 x 值所属的箱子的索引（对应于 bin_edges）。与 values 的长度相同。binnumber 为 i 表示相应的值介于 (bin_edges[i-1], bin_edges[i]) 之间。

另请参阅

numpy.digitize，numpy.histogram，binned_statistic_2d，binned_statistic_dd

注释

除了最后一个（最右边的）箱子之外，所有箱子都是半开的。换句话说，如果 bins 是 [1, 2, 3, 4]，则第一个箱子是 [1, 2)（包括 1，但不包括 2），第二个箱子是 [2, 3)。但是，最后一个箱子是 [3, 4]，它包括 4。

在 0.11.0 版本中添加。

示例

在浏览器中试一试！

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

首先是一些基本示例

在给定样本的范围内创建两个均匀间隔的箱子，并对每个箱子中相应的值求和

>>> values = [1.0, 1.0, 2.0, 1.5, 3.0]
>>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2)
BinnedStatisticResult(statistic=array([4. , 4.5]),
        bin_edges=array([1., 4., 7.]), binnumber=array([1, 1, 1, 2, 2]))

还可以传递多个值数组。统计量是针对每个集合独立计算的

>>> values = [[1.0, 1.0, 2.0, 1.5, 3.0], [2.0, 2.0, 4.0, 3.0, 6.0]]
>>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2)
BinnedStatisticResult(statistic=array([[4. , 4.5],
       [8. , 9. ]]), bin_edges=array([1., 4., 7.]),
       binnumber=array([1, 1, 1, 2, 2]))

>>> stats.binned_statistic([1, 2, 1, 2, 4], np.arange(5), statistic='mean',
...                        bins=3)
BinnedStatisticResult(statistic=array([1., 2., 4.]),
        bin_edges=array([1., 2., 3., 4.]),
        binnumber=array([1, 2, 1, 2, 3]))

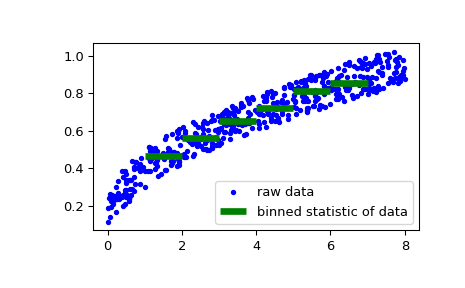
作为第二个示例，我们现在生成一些帆船速度作为风速函数的随机数据，然后确定我们的船在特定风速下的速度有多快

>>> rng = np.random.default_rng()
>>> windspeed = 8 * rng.random(500)
>>> boatspeed = .3 * windspeed**.5 + .2 * rng.random(500)
>>> bin_means, bin_edges, binnumber = stats.binned_statistic(windspeed,
...                 boatspeed, statistic='median', bins=[1,2,3,4,5,6,7])
>>> plt.figure()
>>> plt.plot(windspeed, boatspeed, 'b.', label='raw data')
>>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=5,
...            label='binned statistic of data')
>>> plt.legend()

现在我们可以使用 binnumber 来选择所有风速低于 1 的数据点

>>> low_boatspeed = boatspeed[binnumber == 0]

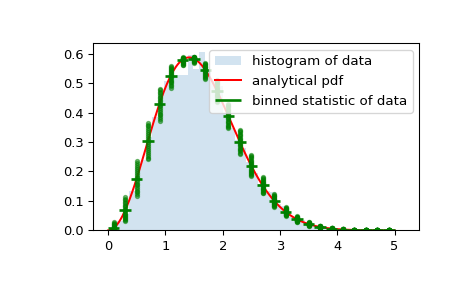
作为最后一个示例，我们将使用 bin_edges 和 binnumber 来绘制一个分布图，该分布图显示每个箱子的平均值和围绕平均值的分布，并在常规直方图和概率分布函数之上显示

>>> x = np.linspace(0, 5, num=500)
>>> x_pdf = stats.maxwell.pdf(x)
>>> samples = stats.maxwell.rvs(size=10000)

>>> bin_means, bin_edges, binnumber = stats.binned_statistic(x, x_pdf,
...         statistic='mean', bins=25)
>>> bin_width = (bin_edges[1] - bin_edges[0])
>>> bin_centers = bin_edges[1:] - bin_width/2

>>> plt.figure()
>>> plt.hist(samples, bins=50, density=True, histtype='stepfilled',
...          alpha=0.2, label='histogram of data')
>>> plt.plot(x, x_pdf, 'r-', label='analytical pdf')
>>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=2,
...            label='binned statistic of data')
>>> plt.plot((binnumber - 0.5) * bin_width, x_pdf, 'g.', alpha=0.5)
>>> plt.legend(fontsize=10)
>>> plt.show()

返回在新标签页中打开