scipy.stats.Uniform.

plot#

Uniform.plot(x='x', y=None, *, t=None, ax=None)[source]#

绘制分布的函数。

用于快速可视化随机变量底层分布的便捷函数。

参数:

x, ystr, 可选: 字符串，指示用作横坐标和纵坐标（水平和垂直坐标）的量。默认值为 'x' (随机变量的域) 和 'pdf' (概率密度函数) (连续) 或 'pdf' (概率密度函数) (离散)。有效值为：‘x’、‘pdf’、‘pmf’、‘cdf’、‘ccdf’、‘icdf’、‘iccdf’、‘logpdf’、‘logpmf’、‘logcdf’、‘logccdf’、‘ilogcdf’、‘ilogccdf’。
t3 元组 (str, float, float)，可选: 元组，指示绘制这些量的限制范围。如果域是无限的，则默认值为 ('cdf', 0.0005, 0.9995)，指示要显示分布的中心 99.9%；否则，使用支持的端点，如果它们是有限的。有效值为：‘x’、‘cdf’、‘ccdf’、‘icdf’、‘iccdf’、‘logcdf’、‘logccdf’、‘ilogcdf’、‘ilogccdf’。
axmatplotlib.axes, 可选: 要在其上生成绘图的轴。如果未提供，则使用当前轴。

返回:

示例

使用所需的参数实例化分布

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> X = stats.Normal(mu=1., sigma=2.)

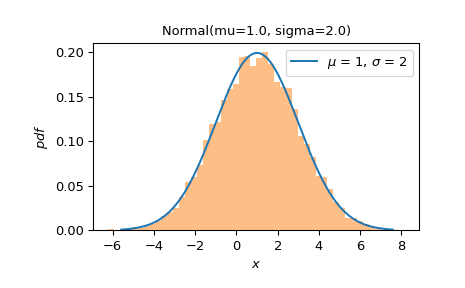
在分布的中心 99.9% 上绘制 PDF。与随机样本的直方图进行比较。

>>> ax = X.plot()
>>> sample = X.sample(10000)
>>> ax.hist(sample, density=True, bins=50, alpha=0.5)
>>> plt.show()

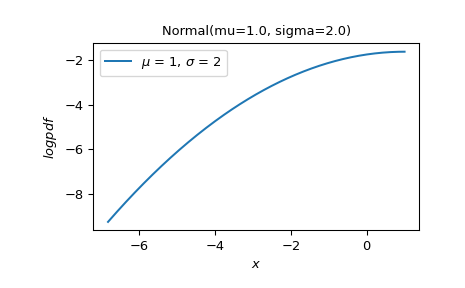
在左尾中将 logpdf(x) 绘制为 x 的函数，其中 CDF 的对数介于 -10 和 np.log(0.5) 之间。

>>> X.plot('x', 'logpdf', t=('logcdf', -10, np.log(0.5)))
>>> plt.show()

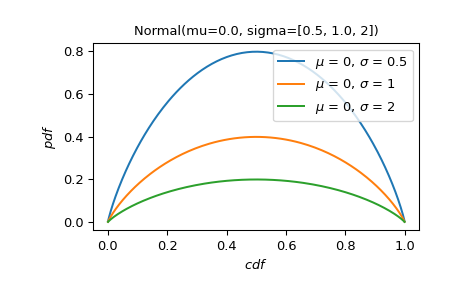
将正态分布的 PDF 绘制为 CDF 的函数，用于各种比例参数值。

>>> X = stats.Normal(mu=0., sigma=[0.5, 1., 2])
>>> X.plot('cdf', 'pdf')
>>> plt.show()