scipy.special.spence

scipy.special.spence(z, out=None) = <ufunc 'spence'>

Spence 函数，也称为双对数函数。

它的定义为

\[\int_1^z \frac{\log(t)}{1 - t}dt\]

对于复数 \(z\)，其中积分的轮廓被选择为避开对数的分支切割。Spence 函数在除了负实轴之外的任何地方都是解析的，在负实轴上它具有分支切割。

参数:

zarray_like

要评估 Spence 函数的点

outndarray，可选

用于函数结果的可选输出数组

返回值:

s标量或 ndarray

Spence 函数的计算值

注释

有一种不同的约定，它通过积分定义 Spence 函数

\[-\int_0^z \frac{\log(1 - t)}{t}dt;\]

这就是我们的 spence(1 - z)。

示例

在您的浏览器中尝试！

>>> import numpy as np
>>> from scipy.special import spence
>>> import matplotlib.pyplot as plt

该函数为复数输入定义

>>> spence([1-1j, 1.5+2j, 3j, -10-5j])
array([-0.20561676+0.91596559j, -0.86766909-1.39560134j,
       -0.59422064-2.49129918j, -1.14044398+6.80075924j])

对于分支切割上的复数输入，即负实轴，该函数返回具有正虚部的 z 的极限。例如，在下面的示例中，请注意 z = -2 和 z = -2 - 1e-8j 的输出的虚部的符号变化

>>> spence([-2 + 1e-8j, -2, -2 - 1e-8j])
array([2.32018041-3.45139229j, 2.32018042-3.4513923j ,
       2.32018041+3.45139229j])

该函数为分支切割上的实数输入返回 nan

>>> spence(-1.5)
nan

验证一些特定值：spence(0) = pi**2/6，spence(1) = 0 和 spence(2) = -pi**2/12。

>>> spence([0, 1, 2])
array([ 1.64493407,  0.        , -0.82246703])
>>> np.pi**2/6, -np.pi**2/12
(1.6449340668482264, -0.8224670334241132)

验证恒等式

spence(z) + spence(1 - z) = pi**2/6 - log(z)*log(1 - z)

>>> z = 3 + 4j
>>> spence(z) + spence(1 - z)
(-2.6523186143876067+1.8853470951513935j)
>>> np.pi**2/6 - np.log(z)*np.log(1 - z)
(-2.652318614387606+1.885347095151394j)

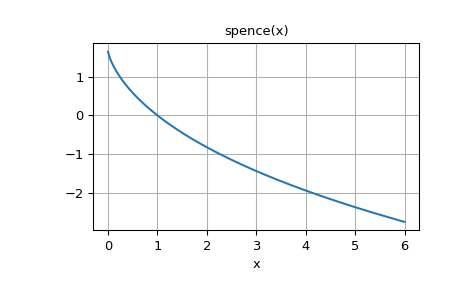
绘制正实数输入的函数。

>>> fig, ax = plt.subplots()
>>> x = np.linspace(0, 6, 400)
>>> ax.plot(x, spence(x))
>>> ax.grid()
>>> ax.set_xlabel('x')
>>> ax.set_title('spence(x)')
>>> plt.show()

返回在新标签页中打开