scipy.special.mathieu_sem#

scipy.special.mathieu_sem(m, q, x, out=None) = <ufunc 'mathieu_sem'>#

奇马蒂厄函数及其导数

返回 m 阶和 q 参数的奇马蒂厄函数 se_m(x, q)，在 x 处求值（以度为单位）。同时返回 se_m(x, q) 相对于 x 的导数。

参数:

marray_like: 函数的阶数
qarray_like: 函数的参数
xarray_like: 函数的参数，以度为单位，而不是弧度。
outndarray 元组, 可选: 函数结果的可选输出数组

返回:

y标量或 ndarray: 函数的值
yp标量或 ndarray: 相对于 x 的导数值

参见

mathieu_a, mathieu_b, mathieu_cem

备注

奇马蒂厄函数是马蒂厄微分方程的解

\[\frac{d^2y}{dx^2} + (b_m - 2q \cos(2x))y = 0\]

对于该方程，特征数 \(b_m\) (使用 mathieu_b 计算) 产生一个奇的周期解 \(y(x)\)，其周期为 180 度（对于偶数 \(m\)）或 360 度（对于奇数 \(m\)）。

参考文献

[1]

‘Mathieu function’. Wikipedia. https://en.wikipedia.org/wiki/Mathieu_function

示例

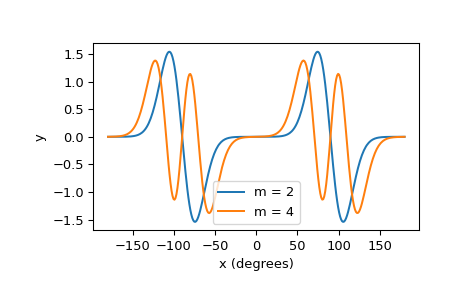
绘制 2 阶和 4 阶的奇马蒂厄函数。

>>> import numpy as np
>>> from scipy import special
>>> import matplotlib.pyplot as plt
>>> m = np.asarray([2, 4])
>>> q = 50
>>> x = np.linspace(-180, 180, 300)[:, np.newaxis]
>>> y, _ = special.mathieu_sem(m, q, x)
>>> plt.plot(x, y)
>>> plt.xlabel('x (degrees)')
>>> plt.ylabel('y')
>>> plt.legend(('m = 2', 'm = 4'))

由于 2 阶和 4 阶是偶数，因此每个函数的周期为 180 度。

../../_images/scipy-special-mathieu_sem-1.png