scipy.signal.

unit_impulse#

scipy.signal.unit_impulse(shape, idx=None, dtype=<class 'float'>)[source]#

单位脉冲信号（离散狄拉克函数）或单位基向量。

参数:
shapeint 或 int 元组

输出中的样本数（1-D），或表示输出形状（N-D）的元组。

idxNone 或 int 或 int 元组 或 ‘mid’，可选

值为 1 的索引。如果为 None，默认为第 0 个元素。如果 idx='mid'，则脉冲将以所有维度中的 shape // 2 为中心。如果为 int，则脉冲将位于所有维度中的 idx。

dtype数据类型，可选

数组所需的数据类型，例如 numpy.int8。默认为 numpy.float64。

返回:
yndarray

包含脉冲信号的输出数组。

备注

在数字信号处理文献中，单位脉冲信号通常由克罗内克 delta 表示。[1] 即，除了在第 \(k\) 个样本处为一以外，其他地方都为零的信号 \(u_k[n]\) 可以表示为

\[u_k[n] = \delta[n-k] \equiv \delta_{n,k}\ .\]

此外，单位脉冲通常被解释为连续时间狄拉克分布的离散时间版本。[2]

参考文献

0.19.0 版本新增。

示例

第 0 个元素处的脉冲（\(\\delta[n]\)）

>>> from scipy import signal
>>> signal.unit_impulse(8)
array([ 1.,  0.,  0.,  0.,  0.,  0.,  0.,  0.])

偏移 2 个样本的脉冲（\(\\delta[n-2]\)）

>>> signal.unit_impulse(7, 2)
array([ 0.,  0.,  1.,  0.,  0.,  0.,  0.])

2 维居中脉冲

>>> signal.unit_impulse((3, 3), 'mid')
array([[ 0.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  0.]])

使用广播在 (2, 2) 处的脉冲

>>> signal.unit_impulse((4, 4), 2)
array([[ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.],
       [ 0.,  0.,  0.,  0.]])

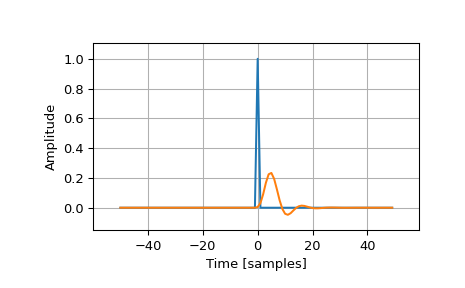
绘制 4 阶巴特沃斯低通滤波器的脉冲响应

>>> imp = signal.unit_impulse(100, 'mid')
>>> b, a = signal.butter(4, 0.2)
>>> response = signal.lfilter(b, a, imp)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> plt.plot(np.arange(-50, 50), imp)
>>> plt.plot(np.arange(-50, 50), response)
>>> plt.margins(0.1, 0.1)
>>> plt.xlabel('Time [samples]')
>>> plt.ylabel('Amplitude')
>>> plt.grid(True)
>>> plt.show()
../../_images/scipy-signal-unit_impulse-1.png
本页内容