scipy.optimize.

bracket#

scipy.optimize.bracket(func, xa=0.0, xb=1.0, args=(), grow_limit=110.0, maxiter=1000)[source]#

确定函数的最小值区间。

给定一个函数和不同的初始点，沿下降方向（由初始点定义）搜索并返回三个点，这些点构成函数最小值的区间。

参数:

func可调用对象 f(x,*args): 要最小化的目标函数。
xa, xb浮点数, 可选: 初始点。 xa 默认为 0.0，xb 默认为 1.0。局部最小值不必包含在此区间内。
args元组, 可选: 附加参数（如果存在），传递给 func。
grow_limit浮点数, 可选: 最大增长限制。默认为 110.0
maxiter整数, 可选: 要执行的最大迭代次数。默认为 1000。

返回:

xa, xb, xc浮点数: 区间的最终点。
fa, fb, fc浮点数: 区间点处的目标函数值。
funcalls整数: 函数评估次数。

引发:

BracketError: 如果在算法终止前未找到有效区间。有关有效区间的条件，请参见注释。

注释

该算法试图找到三个严格有序的点（即 \(x_a < x_b < x_c\) 或 \(x_c < x_b < x_a\)），满足 \(f(x_b) ≤ f(x_a)\) 和 \(f(x_b) ≤ f(x_c)\)，其中一个不等式必须严格满足，且所有 \(x_i\) 都必须是有限的。

示例

此函数可以找到函数的向下凸区域

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.optimize import bracket
>>> def f(x):
...     return 10*x**2 + 3*x + 5
>>> x = np.linspace(-2, 2)
>>> y = f(x)
>>> init_xa, init_xb = 0.1, 1
>>> xa, xb, xc, fa, fb, fc, funcalls = bracket(f, xa=init_xa, xb=init_xb)
>>> plt.axvline(x=init_xa, color="k", linestyle="--")
>>> plt.axvline(x=init_xb, color="k", linestyle="--")
>>> plt.plot(x, y, "-k")
>>> plt.plot(xa, fa, "bx")
>>> plt.plot(xb, fb, "rx")
>>> plt.plot(xc, fc, "bx")
>>> plt.show()

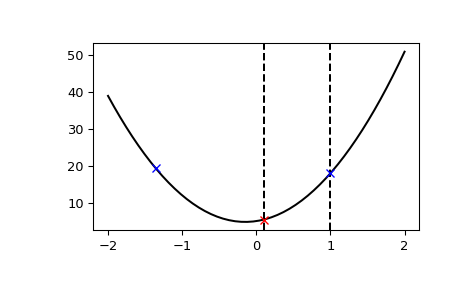
../../_images/scipy-optimize-bracket-1_00_00.png

请注意，两个初始点都在最小值的右侧，第三个点是在“下降”方向（函数看起来正在减小（向左））找到的。最终点是严格有序的，并且中间点的函数值小于端点的函数值；由此可知，最小值必须位于该区间内。