scipy.interpolate.SmoothBivariateSpline.
ev#
- SmoothBivariateSpline.ev(xi, yi, dx=0, dy=0)[source]#
在点上评估样条
返回在
(xi[i], yi[i]), i=0,...,len(xi)-1处的插值。- 参数:
- xi, yiarray_like
输入坐标。 遵循标准的 Numpy 广播。 轴的顺序与
np.meshgrid(..., indexing="ij")一致,与默认顺序np.meshgrid(..., indexing="xy")不一致。- dxint, optional
x-导数的阶数
在 0.14.0 版本中添加。
- dyint, optional
y-导数的阶数
在 0.14.0 版本中添加。
示例
假设我们想要双线性插值一个二维指数衰减函数。
>>> import numpy as np >>> from scipy.interpolate import RectBivariateSpline >>> def f(x, y): ... return np.exp(-np.sqrt((x / 2) ** 2 + y**2))
我们在粗网格上对函数进行采样并设置插值器。 请注意,meshgrid 的默认
indexing="xy"将导致插值后出现意外(转置)结果。>>> xarr = np.linspace(-3, 3, 21) >>> yarr = np.linspace(-3, 3, 21) >>> xgrid, ygrid = np.meshgrid(xarr, yarr, indexing="ij") >>> zdata = f(xgrid, ygrid) >>> rbs = RectBivariateSpline(xarr, yarr, zdata, kx=1, ky=1)
接下来,我们使用插值在更精细的网格上沿坐标空间的对角线切片对函数进行采样。
>>> xinterp = np.linspace(-3, 3, 201) >>> yinterp = np.linspace(3, -3, 201) >>> zinterp = rbs.ev(xinterp, yinterp)
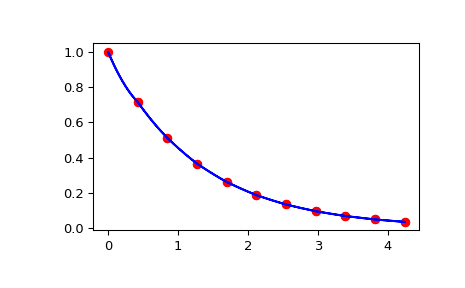
并检查插值是否作为切片上距原点距离的函数通过函数评估。
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(1, 1, 1) >>> ax1.plot(np.sqrt(xarr**2 + yarr**2), np.diag(zdata), "or") >>> ax1.plot(np.sqrt(xinterp**2 + yinterp**2), zinterp, "-b") >>> plt.show()