scipy.interpolate.SmoothBivariateSpline.

__call__

SmoothBivariateSpline.__call__(x, y, dx=0, dy=0, grid=True)

在给定位置评估样条或其导数。

参数:

x, yarray_like

输入坐标。

如果 grid 为 False，则在点 (x[i], y[i]), i=0, ..., len(x)-1 处评估样条。遵守标准 Numpy 广播。

如果 grid 为 True：在由坐标数组 x、y 定义的网格点处评估样条。数组必须按升序排序。

轴的排序与 np.meshgrid(..., indexing="ij") 一致，与默认排序 np.meshgrid(..., indexing="xy") 不一致。

dxint

x 导数的阶数

在版本 0.14.0 中添加。

dyint

y 导数的阶数

在版本 0.14.0 中添加。

gridbool

是否在由输入数组跨越的网格上评估结果，或在由输入数组指定的点处评估结果。

在版本 0.14.0 中添加。

示例

在浏览器中尝试一下！

假设我们要对二维指数衰减函数进行双线性插值。

>>> import numpy as np
>>> from scipy.interpolate import RectBivariateSpline

我们在粗网格上对函数进行采样。请注意，meshgrid 的默认索引“xy”将在插值后产生意外的（转置）结果。

>>> xarr = np.linspace(-3, 3, 100)
>>> yarr = np.linspace(-3, 3, 100)
>>> xgrid, ygrid = np.meshgrid(xarr, yarr, indexing="ij")

要插值的函数沿一个轴比另一个轴衰减更快。

>>> zdata = np.exp(-np.sqrt((xgrid / 2) ** 2 + ygrid**2))

接下来，我们使用插值在更精细的网格上进行采样（kx=ky=1 用于双线性）。

>>> rbs = RectBivariateSpline(xarr, yarr, zdata, kx=1, ky=1)
>>> xarr_fine = np.linspace(-3, 3, 200)
>>> yarr_fine = np.linspace(-3, 3, 200)
>>> xgrid_fine, ygrid_fine = np.meshgrid(xarr_fine, yarr_fine, indexing="ij")
>>> zdata_interp = rbs(xgrid_fine, ygrid_fine, grid=False)

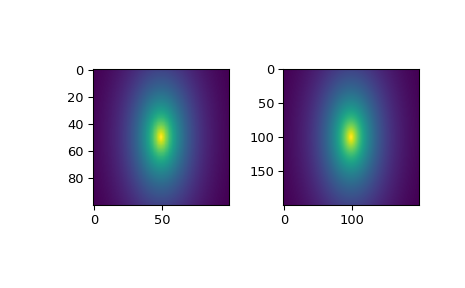
并通过绘制两者来检查结果是否与输入一致。

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 2, 1, aspect="equal")
>>> ax2 = fig.add_subplot(1, 2, 2, aspect="equal")
>>> ax1.imshow(zdata)
>>> ax2.imshow(zdata_interp)
>>> plt.show()

返回在新标签页中打开