scipy.integrate.

solve_bvp#

scipy.integrate.solve_bvp(fun, bc, x, y, p=None, S=None, fun_jac=None, bc_jac=None, tol=0.001, max_nodes=1000, verbose=0, bc_tol=None)[源代码]#

求解常微分方程组的边值问题。

此函数对受两点边界条件约束的一阶常微分方程组进行数值求解

dy / dx = f(x, y, p) + S * y / (x - a), a <= x <= b
bc(y(a), y(b), p) = 0

其中 x 是一个一维自变量，y(x) 是一个 n 维向量值函数，p 是一个 k 维未知参数向量，需要与 y(x) 一起求出。为了确定问题，必须有 n + k 个边界条件，即 bc 必须是一个 (n + k) 维函数。

系统右侧的最后一个奇异项是可选的。它由一个 n 乘 n 矩阵 S 定义，使得解必须满足 S y(a) = 0。此条件将在迭代期间强制执行，因此它不能与边界条件矛盾。有关在数值求解 BVP 时如何处理此项的解释，请参见[2]。

复数域中的问题也可以解决。在这种情况下，y 和 p 被认为是复数，f 和 bc 被假定为复数值函数，但 x 保持实数。请注意，f 和 bc 必须是复数可微的（满足柯西-黎曼方程[4]），否则您应该分别重写实部和虚部的问题。要解决复数域中的问题，请传递一个具有复杂数据类型的 y 的初始猜测（参见下文）。

参数：
fun可调用对象

系统右侧。调用签名是 fun(x, y)，如果存在参数，则是 fun(x, y, p)。所有参数都是 ndarray：x 的形状为 (m,)，y 的形状为 (n, m)，表示 y[:, i] 对应于 x[i]，p 的形状为 (k,)。返回值必须是形状为 (n, m) 且与 y 布局相同的数组。

bc可调用对象

评估边界条件残差的函数。调用签名是 bc(ya, yb)，如果存在参数，则是 bc(ya, yb, p)。所有参数都是 ndarray：ya 和 yb 的形状为 (n,)，p 的形状为 (k,)。返回值必须是形状为 (n + k,) 的数组。

xarray_like，形状 (m,)

初始网格。必须是严格递增的实数序列，其中 x[0]=a 和 x[-1]=b。

yarray_like，形状 (n, m)

网格节点处函数值的初始猜测，第 i 列对应于 x[i]。对于复数域中的问题，即使初始猜测是纯实数，也请传递具有复数数据类型的 y。

parray_like，形状 (k,) 或 None，可选

未知参数的初始猜测。如果为 None（默认），则假定问题不依赖于任何参数。

Sarray_like，形状 (n, n) 或 None

定义奇异项的矩阵。如果为 None（默认），则在没有奇异项的情况下求解问题。

fun_jac可调用对象或 None，可选

计算 f 对 y 和 p 的导数的函数。调用签名是 fun_jac(x, y)，如果存在参数，则是 fun_jac(x, y, p)。返回值必须包含 1 或 2 个元素，按以下顺序排列

  • df_dy : array_like，形状 (n, n, m)，其中元素 (i, j, q) 等于 d f_i(x_q, y_q, p) / d (y_q)_j。

  • df_dp : array_like，形状 (n, k, m)，其中元素 (i, j, q) 等于 d f_i(x_q, y_q, p) / d p_j。

此处 q 表示定义 x 和 y 的节点，而 i 和 j 表示向量分量。如果问题在没有未知参数的情况下求解，则不应返回 df_dp。

如果 fun_jac 为 None（默认），则导数将通过向前有限差分进行估计。

bc_jac可调用对象或 None，可选

计算 bc 对 ya、yb 和 p 的导数的函数。调用签名是 bc_jac(ya, yb)，如果存在参数，则是 bc_jac(ya, yb, p)。返回值必须包含 2 或 3 个元素，按以下顺序排列

  • dbc_dya : array_like，形状 (n, n)，其中元素 (i, j) 等于 d bc_i(ya, yb, p) / d ya_j。

  • dbc_dyb : array_like，形状 (n, n)，其中元素 (i, j) 等于 d bc_i(ya, yb, p) / d yb_j。

  • dbc_dp : array_like，形状 (n, k)，其中元素 (i, j) 等于 d bc_i(ya, yb, p) / d p_j。

如果问题在没有未知参数的情况下求解，则不应返回 dbc_dp。

如果 bc_jac 为 None（默认），则导数将通过向前有限差分进行估计。

tol浮点数，可选

所需解的容差。如果我们将 r = y' - f(x, y) 定义为找到的解，则求解器尝试在每个网格区间上达到 norm(r / (1 + abs(f)) < tol，其中 norm 以均方根意义估计（使用数值积分公式）。默认为 1e-3。

max_nodes整数，可选

网格节点的最大允许数量。如果超过此值，算法将终止。默认为 1000。

verbose{0, 1, 2}，可选

算法的详细程度级别

  • 0（默认）: 静默工作。

  • 1 : 显示终止报告。

  • 2 : 在迭代过程中显示进度。

bc_tol浮点数，可选

边界条件残差的所需绝对容差：bc 值应逐分量满足 abs(bc) < bc_tol。默认等于 tol。允许最多 10 次迭代以达到此容差。

返回：
具有以下字段的 Bunch 对象
solPPoly

找到的 y 的解，作为 scipy.interpolate.PPoly 实例，一个 C1 连续的三次样条。

pndarray 或 None，形状 (k,)

找到的参数。如果问题中不存在参数，则为 None。

xndarray，形状 (m,)

最终网格的节点。

yndarray，形状 (n, m)

网格节点处的解值。

ypndarray，形状 (n, m)

网格节点处的解导数。

rms_residualsndarray，形状 (m - 1,)

每个网格区间上的相对残差的 RMS 值（参见 tol 参数的描述）。

niter整数

已完成的迭代次数。

status整数

算法终止原因

  • 0: 算法收敛到所需精度。

  • 1: 超出了网格节点的最大数量。

  • 2: 求解搭配系统时遇到奇异雅可比矩阵。

message字符串

终止原因的文字描述。

success布尔值

如果算法收敛到所需精度（status=0），则为 True。

备注

此函数实现了一个四阶搭配算法，其残差控制类似于[1]。搭配系统通过阻尼牛顿法求解，其仿射不变判据函数如[3]所述。

请注意，在[1]中，积分残差的定义没有通过区间长度进行归一化。因此，它们的定义与此处使用的定义相差一个 h**0.5（h 是区间长度）的乘数。

在版本 0.18.0 中添加。

参考文献

[1] (1,2)

J. Kierzenka, L. F. Shampine, “A BVP Solver Based on Residual Control and the Maltab PSE”, ACM Trans. Math. Softw., Vol. 27, Number 3, pp. 299-316, 2001.

[2]

L.F. Shampine, P. H. Muir and H. Xu, “A User-Friendly Fortran BVP Solver”, J. Numer. Anal., Ind. Appl. Math. (JNAIAM), Vol. 1, Number 2, pp. 201-217, 2006.

[3]

U. Ascher, R. Mattheij and R. Russell “Numerical Solution of Boundary Value Problems for Ordinary Differential Equations”, Philidelphia, PA: Society for Industrial and Applied Mathematics, 1995. DOI:10.1137/1.9781611971231

示例

在第一个示例中，我们求解布拉图问题

y'' + k * exp(y) = 0
y(0) = y(1) = 0

对于 k = 1。

我们将方程重写为一阶系统并实现其右侧评估

y1' = y2
y2' = -exp(y1)

>>> import numpy as np
>>> def fun(x, y):
...     return np.vstack((y[1], -np.exp(y[0])))

实现边界条件残差的评估

>>> def bc(ya, yb):
...     return np.array([ya[0], yb[0]])

定义包含 5 个节点的初始网格

>>> x = np.linspace(0, 1, 5)

已知此问题有两个解。为了获得这两个解，我们对 y 使用两个不同的初始猜测。我们用下标 a 和 b 表示它们。

>>> y_a = np.zeros((2, x.size))
>>> y_b = np.zeros((2, x.size))
>>> y_b[0] = 3

现在我们准备运行求解器。

>>> from scipy.integrate import solve_bvp
>>> res_a = solve_bvp(fun, bc, x, y_a)
>>> res_b = solve_bvp(fun, bc, x, y_b)

让我们绘制找到的两个解。我们利用解的样条形式来生成平滑的绘图。

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot_a = res_a.sol(x_plot)[0]
>>> y_plot_b = res_b.sol(x_plot)[0]
>>> import matplotlib.pyplot as plt
>>> plt.plot(x_plot, y_plot_a, label='y_a')
>>> plt.plot(x_plot, y_plot_b, label='y_b')
>>> plt.legend()
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()
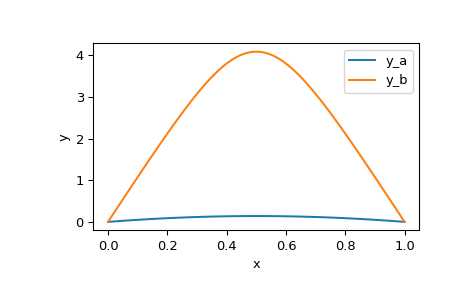
../../_images/scipy-integrate-solve_bvp-1_00_00.png

我们看到这两个解的形状相似，但在尺度上差异显著。

在第二个示例中，我们求解一个简单的斯图姆-刘维尔问题

y'' + k**2 * y = 0
y(0) = y(1) = 0

已知非平凡解 y = A * sin(k * x) 对于 k = pi * n（其中 n 为整数）是可能的。为了将归一化常数 A = 1 确定下来，我们添加一个边界条件

y'(0) = k

再次，我们将方程重写为一阶系统并实现其右侧评估

y1' = y2
y2' = -k**2 * y1

>>> def fun(x, y, p):
...     k = p[0]
...     return np.vstack((y[1], -k**2 * y[0]))

请注意，参数 p 作为向量传递（在我们的例子中只包含一个元素）。

实现边界条件

>>> def bc(ya, yb, p):
...     k = p[0]
...     return np.array([ya[0], yb[0], ya[1] - k])

设置 y 的初始网格和猜测。我们的目标是找到 k = 2 * pi 的解，为此我们将 y 的值设置为大约遵循 sin(2 * pi * x)

>>> x = np.linspace(0, 1, 5)
>>> y = np.zeros((2, x.size))
>>> y[0, 1] = 1
>>> y[0, 3] = -1

运行求解器，将 6 作为 k 的初始猜测。

>>> sol = solve_bvp(fun, bc, x, y, p=[6])

我们看到找到的 k 近似正确

>>> sol.p[0]
6.28329460046

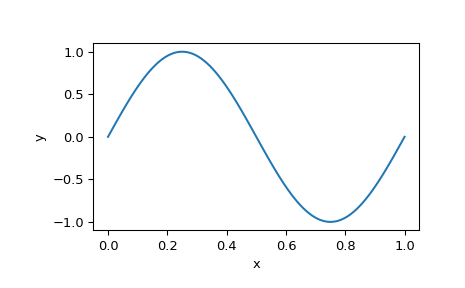
最后，绘制解以查看预期的正弦曲线

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot = sol.sol(x_plot)[0]
>>> plt.plot(x_plot, y_plot)
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()
../../_images/scipy-integrate-solve_bvp-1_01_00.png
本页内容