scipy.integrate.

quad_vec#

scipy.integrate.quad_vec(f, a, b, epsabs=1e-200, epsrel=1e-08, norm='2', cache_size=100000000.0, limit=10000, workers=1, points=None, quadrature=None, full_output=False, *, args=())[source]#

向量值函数的自适应积分。

参数:
f可调用对象

要积分的向量值函数 f(x)。

a浮点数

起始点。

b浮点数

终点。

epsabs浮点数, 可选

绝对容差。

epsrel浮点数, 可选

相对容差。

norm{'max', '2'}, 可选

用于误差估计的向量范数。

cache_size整数, 可选

用于记忆化的字节数。

limit浮点数或整数, 可选

自适应算法中使用的子区间数的上限。

workers整数或类映射可调用对象, 可选

如果 workers 是一个整数，则部分计算将并行完成，细分为这么多任务（使用 multiprocessing.pool.Pool）。提供 -1 以使用进程可用的所有核心。或者，提供一个类映射可调用对象，例如 multiprocessing.pool.Pool.map，用于并行评估总体。此评估以 workers(func, iterable) 的形式执行。

points列表, 可选

附加断点列表。

quadrature{'gk21', 'gk15', 'trapezoid'}, 可选

在子区间上使用的求积规则。选项：'gk21'（高斯-克朗罗德 21 点规则），'gk15'（高斯-克朗罗德 15 点规则），'trapezoid'（复合梯形规则）。默认：有限区间使用 'gk21'，（半）无限区间使用 'gk15'。

full_output布尔值, 可选

返回一个附加的 info 对象。

args元组, 可选

要传递给函数的额外参数（如果有）。

版本 1.8.0 中新增。

返回:
res{浮点数, 数组类}

结果的估计值

err浮点数

给定范数下结果的误差估计

info对象

仅当 full_output=True 时返回。具有以下属性的结果对象

success布尔值

积分是否达到目标精度。

status整数

收敛指标：成功 (0)、失败 (1) 和因舍入误差导致失败 (2)。

neval整数

函数评估次数。

intervalsndarray, 形状 (num_intervals, 2)

细分区间的起始点和结束点。

integralsndarray, 形状 (num_intervals, ...)

每个区间的积分。请注意，最多记录 cache_size 个值，并且数组可能包含缺失项的 nan。

errorsndarray, 形状 (num_intervals,)

每个区间的估计积分误差。

注释

该算法主要遵循 QUADPACK 的 DQAG* 算法的实现，实现全局误差控制和自适应细分。

这里的算法与 QUADPACK 方法有一些不同之处

该算法不是一次细分一个区间，而是同时细分 N 个误差最大的区间。这使得积分能够（部分）并行化。

因此，没有实现首先细分“下一个最大”区间的逻辑，我们依赖于上述扩展来避免只集中于“小”区间。

不使用 Wynn epsilon 表外推（QUADPACK 将其用于无限区间）。这是因为这里的算法应该在用户指定范数下处理向量值函数，并且 epsilon 算法对此情况的扩展似乎没有被广泛认同。对于最大范数，可以使用逐元素 Wynn epsilon，但我们在这里不这样做，希望 epsilon 外推主要在特殊情况下有用。

参考文献

[1] R. Piessens, E. de Doncker, QUADPACK (1983)。

示例

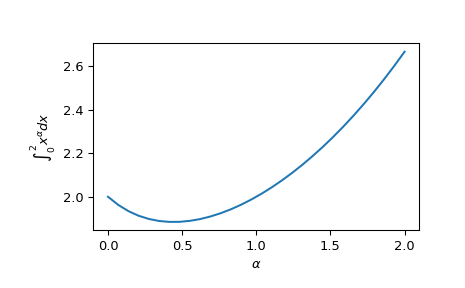
我们可以计算向量值函数的积分

>>> from scipy.integrate import quad_vec
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> alpha = np.linspace(0.0, 2.0, num=30)
>>> f = lambda x: x**alpha
>>> x0, x1 = 0, 2
>>> y, err = quad_vec(f, x0, x1)
>>> plt.plot(alpha, y)
>>> plt.xlabel(r"$\alpha$")
>>> plt.ylabel(r"$\int_{0}^{2} x^\alpha dx$")
>>> plt.show()
../../_images/scipy-integrate-quad_vec-1_00_00.png

当使用参数 workers 时，应确保主模块是导入安全的，例如通过将上述示例重写为

from scipy.integrate import quad_vec
import numpy as np
import matplotlib.pyplot as plt

alpha = np.linspace(0.0, 2.0, num=30)
x0, x1 = 0, 2
def f(x):
    return x**alpha

if __name__ == "__main__":
    y, err = quad_vec(f, x0, x1, workers=2)
本页内容