scipy.integrate.

lebedev_rule#

scipy.integrate.lebedev_rule(n)[源代码]#

Lebedev 积分公式。

计算 Lebedev 积分公式 [1] 的采样点和权重，用于在单位球面上对函数进行积分。

参数:

nint: 积分公式阶数。请参阅“备注”以了解支持的值。

返回:

x形状为 (3, m) 的 ndarray: 单位球面上的采样点，采用笛卡尔坐标系。 m 是与指定阶数对应的“度”；请参阅“备注”。
w形状为 (m,) 的 ndarray: 权重

备注

通过将 [2] 的 Matlab 代码转换为 Python 实现。

可用的阶数（参数 n）为

3, 5, 7, 9, 11, 13, 15, 17,
19, 21, 23, 25, 27, 29, 31, 35,
41, 47, 53, 59, 65, 71, 77, 83,
89, 95, 101, 107, 113, 119, 125, 131

对应的度 m 为

6, 14, 26, 38, 50, 74, 86, 110,
146, 170, 194, 230, 266, 302, 350, 434,
590, 770, 974, 1202, 1454, 1730, 2030, 2354,
2702, 3074, 3470, 3890, 4334, 4802, 5294, 5810

参考文献

[1]

V.I. Lebedev 和 D.N. Laikov。“A quadrature formula for the sphere of the 131st algebraic order of accuracy”。Doklady Mathematics, 第 59 卷，第 3 期，1999 年，第 477-481 页。

[2]

R. Parrish。getLebedevSphere。Matlab Central 文件交换。 https://www.mathworks.com/matlabcentral/fileexchange/27097-getlebedevsphere。

[3]

Bellet, Jean-Baptiste, Matthieu Brachet 和 Jean-Pierre Croisille。“Quadrature and symmetry on the Cubed Sphere。”Journal of Computational and Applied Mathematics 409 (2022): 114142。 DOI:10.1016/j.cam.2022.114142。

示例

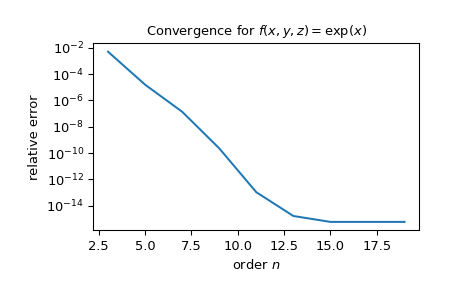
[3] 中给出的一个示例是对半径为 \(1\) 的球体上函数 \(f(x, y, z) = \exp(x)\) 进行积分；参考值为 14.7680137457653。展示随着阶数增加收敛到预期结果的过程

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.integrate import lebedev_rule
>>>
>>> def f(x):
...     return np.exp(x[0])
>>>
>>> res = []
>>> orders = np.arange(3, 20, 2)
>>> for n in orders:
...     x, w = lebedev_rule(n)
...     res.append(w @ f(x))
>>>
>>> ref = np.full_like(res, 14.7680137457653)
>>> err = abs(res - ref)/abs(ref)
>>> plt.semilogy(orders, err)
>>> plt.xlabel('order $n$')
>>> plt.ylabel('relative error')
>>> plt.title(r'Convergence for $f(x, y, z) = \exp(x)$')
>>> plt.show()

../../_images/scipy-integrate-lebedev_rule-1.png