scipy.integrate.

cumulative_simpson#

scipy.integrate.cumulative_simpson(y, *, x=None, dx=1.0, axis=-1, initial=None)[源代码]#

使用复合辛普森 1/3 法则对 y(x) 进行累积积分。通过假设每个点与两个相邻点之间存在二次关系，计算每个点的样本积分。

参数:

y类数组: 要积分的值。要求沿 axis 至少有一个点。如果沿 axis 提供的点少于或等于两个，则无法进行辛普森积分，结果将使用 cumulative_trapezoid 计算。
x类数组，可选: 要积分的坐标。必须与 y 具有相同的形状，或者必须是与 y 沿 axis 具有相同长度的一维数组。x 沿 axis 也必须严格递增。如果 x 为 None（默认值），则使用 y 中连续元素之间的间距 dx 进行积分。
dx标量或类数组，可选: y 元素之间的间距。仅在 x 为 None 时使用。可以是浮点数，也可以是与 y 形状相同但沿 axis 长度为 1 的数组。默认值为 1.0。
axis整型，可选: 指定沿其积分的轴。默认值为 -1（最后一个轴）。
initial标量或类数组，可选: 如果给定，则将此值插入返回结果的开头，并将其添加到结果的其余部分。默认值为 None，这意味着不返回 x[0] 处的值，并且 res 沿积分轴比 y 少一个元素。可以是浮点数，也可以是与 y 形状相同但沿 axis 长度为 1 的数组。

返回值:

resndarray: 沿 axis 对 y 进行累积积分的结果。如果 initial 为 None，则形状使得积分轴比 y 少一个值。如果给定 initial，则形状与 y 相同。

另请参阅

numpy.cumsum
cumulative_trapezoid: 使用复合梯形法则进行累积积分
simpson: 使用复合辛普森法则对采样数据进行积分

说明

在 1.12.0 版本中新增。

复合辛普森 1/3 法可用于近似采样输入函数 \(y(x)\) 的定积分 [1]。该方法假设包含任意三个连续采样点的区间上存在二次关系。

考虑三个连续点： \((x_1, y_1), (x_2, y_2), (x_3, y_3)\)。

假设这三个点之间存在二次关系，则 \(x_1\) 和 \(x_2\) 之间子区间的积分由参考文献 [2] 的公式 (8) 给出：

\[\begin{split}\int_{x_1}^{x_2} y(x) dx\ &= \frac{x_2-x_1}{6}\left[\ \left\{3-\frac{x_2-x_1}{x_3-x_1}\right\} y_1 + \ \left\{3 + \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} + \ \frac{x_2-x_1}{x_3-x_1}\right\} y_2\\ - \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} y_3\right]\end{split}\]

通过交换 \(x_1\) 和 \(x_3\) 的位置，可以得到 \(x_2\) 和 \(x_3\) 之间的积分。对每个子区间分别进行积分估算，然后累积求和以获得最终结果。

对于等间距的样本，如果函数是三次或更低阶的多项式 [1] 且子区间数量为偶数，则结果是精确的。否则，积分对于二次或更低阶的多项式是精确的。

参考文献

[1] (1,2)

维基百科页面： https://en.wikipedia.org/wiki/Simpson’s_rule

[2]

Cartwright, Kenneth V. Simpson’s Rule Cumulative Integration with MS Excel and Irregularly-spaced Data. Journal of Mathematical Sciences and Mathematics Education. 12 (2): 1-9

示例

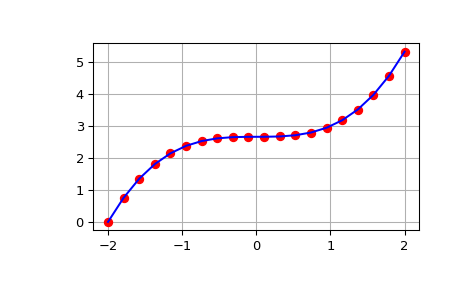
>>> from scipy import integrate
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-2, 2, num=20)
>>> y = x**2
>>> y_int = integrate.cumulative_simpson(y, x=x, initial=0)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y_int, 'ro', x, x**3/3 - (x[0])**3/3, 'b-')
>>> ax.grid()
>>> plt.show()

../../_images/scipy-integrate-cumulative_simpson-1_00_00.png

cumulative_simpson 的输出与迭代调用 simpson 并逐步提高积分上限的输出相似，但并不完全相同。

>>> def cumulative_simpson_reference(y, x):
...     return np.asarray([integrate.simpson(y[:i], x=x[:i])
...                        for i in range(2, len(y) + 1)])
>>>
>>> rng = np.random.default_rng()
>>> x, y = rng.random(size=(2, 10))
>>> x.sort()
>>>
>>> res = integrate.cumulative_simpson(y, x=x)
>>> ref = cumulative_simpson_reference(y, x)
>>> equal = np.abs(res - ref) < 1e-15
>>> equal  # not equal when `simpson` has even number of subintervals
array([False,  True, False,  True, False,  True, False,  True,  True])

这是预料之中的：因为 cumulative_simpson 能够获取比 simpson 更多的信息，它通常可以对子区间上的基础积分产生更准确的估计。