scipy.stats.qmc.

geometric_discrepancy#

scipy.stats.qmc.geometric_discrepancy(sample, method='mindist', metric='euclidean')[source]#

基于几何特性计算给定样本的偏差。

参数:
samplearray_like (n, d)

用于计算偏差的样本。

method{“mindist”, “mst”}, optional

使用的方法。可以是 mindist 表示最小距离（默认）或 mst 表示最小生成树。

metricstr 或 callable, optional

使用的距离度量。有关可用度量和默认值，请参见 scipy.spatial.distance.pdist 的文档。

返回:
discrepancyfloat

偏差（值越高对应于样本均匀性越好）。

参见

discrepancy

注释

偏差可以作为随机样本质量的简单度量。此度量基于样本中点分布的几何特性，例如任意点对之间的最小距离，或最小生成树中的平均边长。

值越高，参数空间的覆盖率越好。请注意，这与 scipy.stats.qmc.discrepancy 不同，在 scipy.stats.qmc.discrepancy 中，较低的值对应于样本的较高质量。

另请注意，在使用此函数比较不同的抽样策略时，必须保持样本大小恒定。

可以从最小生成树计算两个指标：平均边长和边长标准差。使用两个指标比单独使用任何一个指标更能全面了解均匀性，平均值较高且标准差较低更可取（有关简要讨论，请参见 [1]）。此函数目前仅计算平均边长。

参考文献

[1]

Franco J. et al. “Minimum Spanning Tree: A new approach to assess the quality of the design of computer experiments.” Chemometrics and Intelligent Laboratory Systems, 97 (2), pp. 164-169, 2009.

示例

使用最小欧几里得距离（默认值）计算样本的质量

>>> import numpy as np
>>> from scipy.stats import qmc
>>> rng = np.random.default_rng()
>>> sample = qmc.LatinHypercube(d=2, rng=rng).random(50)
>>> qmc.geometric_discrepancy(sample)
0.03708161435687876

使用最小生成树中的平均边长计算质量

>>> qmc.geometric_discrepancy(sample, method='mst')
0.1105149978798376

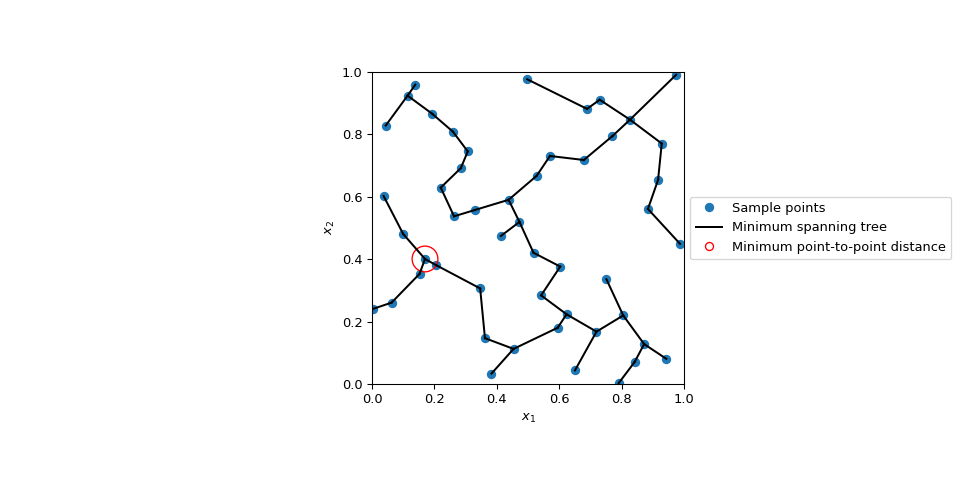
显示最小生成树和距离最小的点

>>> import matplotlib.pyplot as plt
>>> from matplotlib.lines import Line2D
>>> from scipy.sparse.csgraph import minimum_spanning_tree
>>> from scipy.spatial.distance import pdist, squareform
>>> dist = pdist(sample)
>>> mst = minimum_spanning_tree(squareform(dist))
>>> edges = np.where(mst.toarray() > 0)
>>> edges = np.asarray(edges).T
>>> min_dist = np.min(dist)
>>> min_idx = np.argwhere(squareform(dist) == min_dist)[0]
>>> fig, ax = plt.subplots(figsize=(10, 5))
>>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$',
...            xlim=[0, 1], ylim=[0, 1])
>>> for edge in edges:
...     ax.plot(sample[edge, 0], sample[edge, 1], c='k')
>>> ax.scatter(sample[:, 0], sample[:, 1])
>>> ax.add_patch(plt.Circle(sample[min_idx[0]], min_dist, color='red', fill=False))
>>> markers = [
...     Line2D([0], [0], marker='o', lw=0, label='Sample points'),
...     Line2D([0], [0], color='k', label='Minimum spanning tree'),
...     Line2D([0], [0], marker='o', lw=0, markerfacecolor='w', markeredgecolor='r',
...            label='Minimum point-to-point distance'),
... ]
>>> ax.legend(handles=markers, loc='center left', bbox_to_anchor=(1, 0.5));
>>> plt.show()
../../_images/scipy-stats-qmc-geometric_discrepancy-1.png
在此页上