scipy.stats.qmc.

MultinomialQMC#

class scipy.stats.qmc.MultinomialQMC(pvals, n_trials, *, engine=None, rng=None)[source]#

从多项式分布进行 QMC 采样。

参数:
pvalsarray_like (k,)

大小为 k 的概率向量，其中 k 是类别的数量。元素必须是非负的并且总和为 1。

n_trialsint

试验次数。

engineQMCEngine，可选

拟蒙特卡洛引擎采样器。如果为 None，则使用 Sobol。

rngnumpy.random.Generator，可选

伪随机数生成器状态。当 rng 为 None 时，将使用来自操作系统的熵创建一个新的 numpy.random.Generator。除 numpy.random.Generator 之外的类型将传递给 numpy.random.default_rng 以实例化一个 Generator。

在版本 1.15.0 中更改: 作为从使用 numpy.random.RandomState 过渡到 numpy.random.Generator 的 SPEC-007 的一部分，此关键字已从 seed 更改为 rng。在过渡期间，这两个关键字将继续工作，但一次只能指定一个。在过渡期之后，使用 seed 关键字的函数调用将发出警告。在弃用期之后，seed 关键字将被删除。

方法

random([n])

从多项式分布中抽取 n 个 QMC 样本。

示例

让我们定义 3 个类别，对于给定的样本，每个类别的试验总数为 8。每个类别的试验次数由与每个类别关联的 pvals 确定。然后，我们对这个分布采样 64 次。

>>> import matplotlib.pyplot as plt
>>> from scipy.stats import qmc
>>> dist = qmc.MultinomialQMC(
...     pvals=[0.2, 0.4, 0.4], n_trials=10, engine=qmc.Halton(d=1)
... )
>>> sample = dist.random(64)

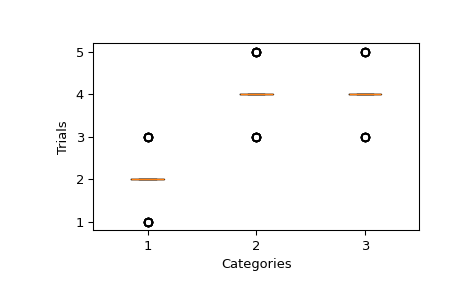
我们可以绘制样本并验证每个类别试验次数的中位数是否遵循 pvals。那将是 pvals * n_trials = [2, 4, 4]。

>>> fig, ax = plt.subplots()
>>> ax.yaxis.get_major_locator().set_params(integer=True)
>>> _ = ax.boxplot(sample)
>>> ax.set(xlabel="Categories", ylabel="Trials")
>>> plt.show()
../../_images/scipy-stats-qmc-MultinomialQMC-1.png
在本页